Classification under Data Contamination with Application to Remote Sensing Image Mis-registration
Paper and Code
Jan 05, 2012
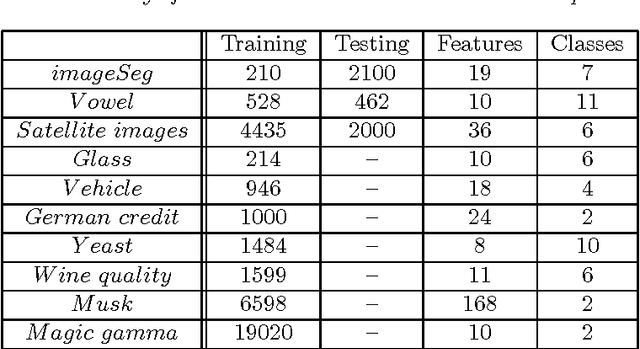
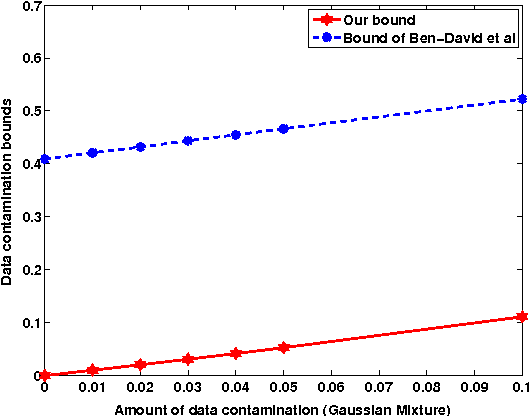
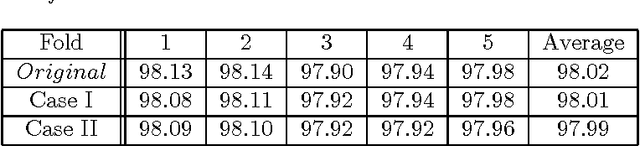
This work is motivated by the problem of image mis-registration in remote sensing and we are interested in determining the resulting loss in the accuracy of pattern classification. A statistical formulation is given where we propose to use data contamination to model and understand the phenomenon of image mis-registration. This model is widely applicable to many other types of errors as well, for example, measurement errors and gross errors etc. The impact of data contamination on classification is studied under a statistical learning theoretical framework. A closed-form asymptotic bound is established for the resulting loss in classification accuracy, which is less than $\epsilon/(1-\epsilon)$ for data contamination of an amount of $\epsilon$. Our bound is sharper than similar bounds in the domain adaptation literature and, unlike such bounds, it applies to classifiers with an infinite Vapnik-Chervonekis (VC) dimension. Extensive simulations have been conducted on both synthetic and real datasets under various types of data contamination, including label flipping, feature swapping and the replacement of feature values with data generated from a random source such as a Gaussian or Cauchy distribution. Our simulation results show that the bound we derive is fairly tight.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge