Transfer Learning for Latent Variable Network Models
Paper and Code
Jun 06, 2024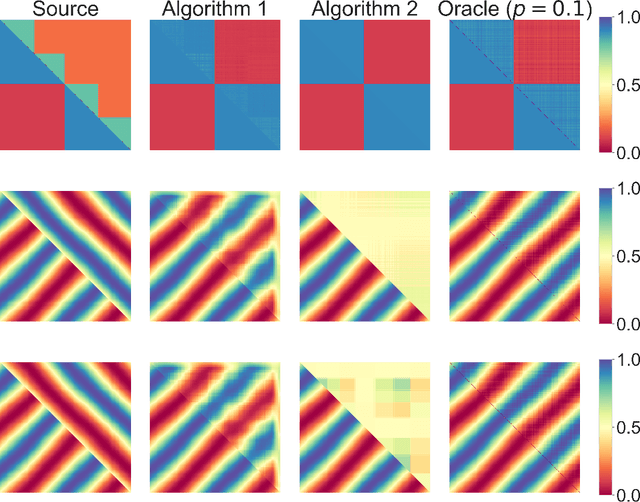
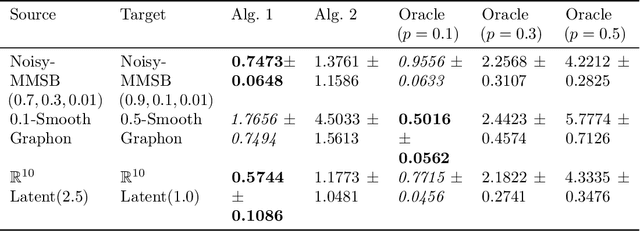
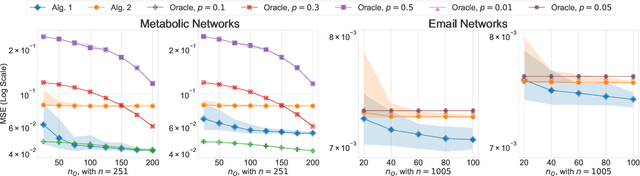
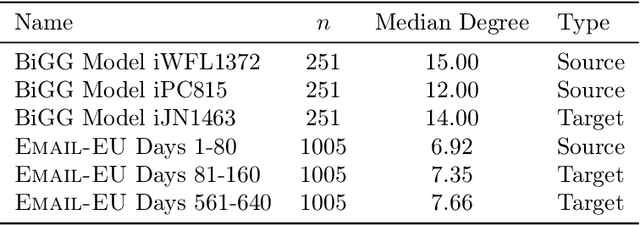
We study transfer learning for estimation in latent variable network models. In our setting, the conditional edge probability matrices given the latent variables are represented by $P$ for the source and $Q$ for the target. We wish to estimate $Q$ given two kinds of data: (1) edge data from a subgraph induced by an $o(1)$ fraction of the nodes of $Q$, and (2) edge data from all of $P$. If the source $P$ has no relation to the target $Q$, the estimation error must be $\Omega(1)$. However, we show that if the latent variables are shared, then vanishing error is possible. We give an efficient algorithm that utilizes the ordering of a suitably defined graph distance. Our algorithm achieves $o(1)$ error and does not assume a parametric form on the source or target networks. Next, for the specific case of Stochastic Block Models we prove a minimax lower bound and show that a simple algorithm achieves this rate. Finally, we empirically demonstrate our algorithm's use on real-world and simulated graph transfer problems.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge