Towards Sample-Optimal Compressive Phase Retrieval with Sparse and Generative Priors
Paper and Code
Jun 29, 2021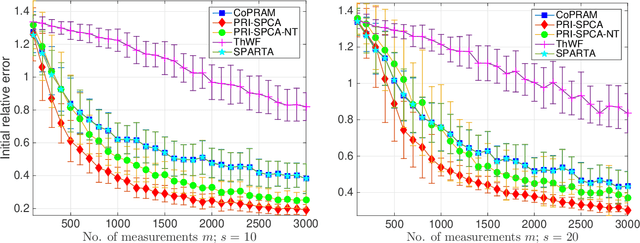
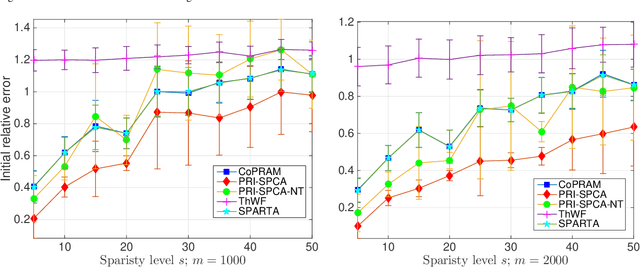
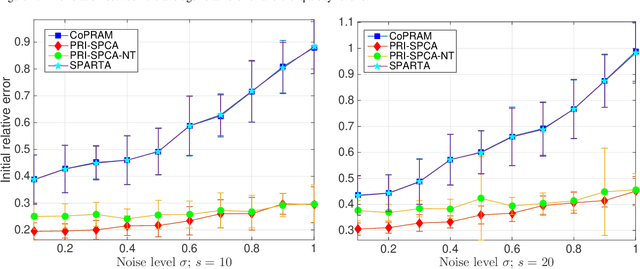
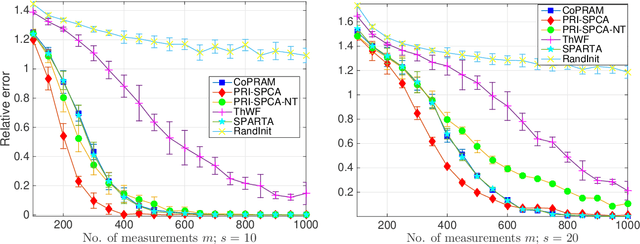
Compressive phase retrieval is a popular variant of the standard compressive sensing problem, in which the measurements only contain magnitude information. In this paper, motivated by recent advances in deep generative models, we provide recovery guarantees with order-optimal sample complexity bounds for phase retrieval with generative priors. We first show that when using i.i.d. Gaussian measurements and an $L$-Lipschitz continuous generative model with bounded $k$-dimensional inputs, roughly $O(k \log L)$ samples suffice to guarantee that the signal is close to any vector that minimizes an amplitude-based empirical loss function. Attaining this sample complexity with a practical algorithm remains a difficult challenge, and a popular spectral initialization method has been observed to pose a major bottleneck. To partially address this, we further show that roughly $O(k \log L)$ samples ensure sufficient closeness between the signal and any {\em globally optimal} solution to an optimization problem designed for spectral initialization (though finding such a solution may still be challenging). We adapt this result to sparse phase retrieval, and show that $O(s \log n)$ samples are sufficient for a similar guarantee when the underlying signal is $s$-sparse and $n$-dimensional, matching an information-theoretic lower bound. While our guarantees do not directly correspond to a practical algorithm, we propose a practical spectral initialization method motivated by our findings, and experimentally observe significant performance gains over various existing spectral initialization methods of sparse phase retrieval.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge