Jiulong Liu
Misspecified Phase Retrieval with Generative Priors
Oct 11, 2022



Abstract:In this paper, we study phase retrieval under model misspecification and generative priors. In particular, we aim to estimate an $n$-dimensional signal $\mathbf{x}$ from $m$ i.i.d.~realizations of the single index model $y = f(\mathbf{a}^T\mathbf{x})$, where $f$ is an unknown and possibly random nonlinear link function and $\mathbf{a} \in \mathbb{R}^n$ is a standard Gaussian vector. We make the assumption $\mathrm{Cov}[y,(\mathbf{a}^T\mathbf{x})^2] \ne 0$, which corresponds to the misspecified phase retrieval problem. In addition, the underlying signal $\mathbf{x}$ is assumed to lie in the range of an $L$-Lipschitz continuous generative model with bounded $k$-dimensional inputs. We propose a two-step approach, for which the first step plays the role of spectral initialization and the second step refines the estimated vector produced by the first step iteratively. We show that both steps enjoy a statistical rate of order $\sqrt{(k\log L)\cdot (\log m)/m}$ under suitable conditions. Experiments on image datasets are performed to demonstrate that our approach performs on par with or even significantly outperforms several competing methods.
Non-Iterative Recovery from Nonlinear Observations using Generative Models
Jun 01, 2022


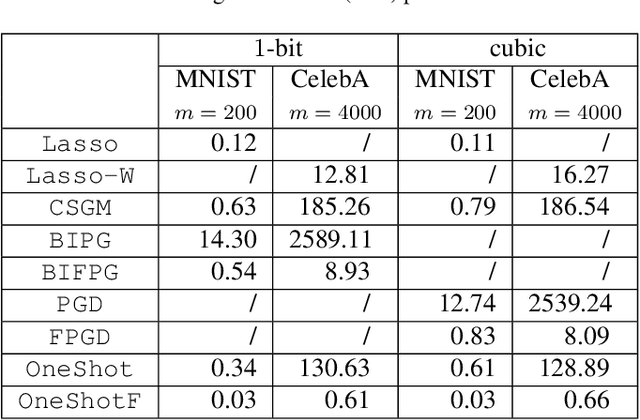
Abstract:In this paper, we aim to estimate the direction of an underlying signal from its nonlinear observations following the semi-parametric single index model (SIM). Unlike conventional compressed sensing where the signal is assumed to be sparse, we assume that the signal lies in the range of an $L$-Lipschitz continuous generative model with bounded $k$-dimensional inputs. This is mainly motivated by the tremendous success of deep generative models in various real applications. Our reconstruction method is non-iterative (though approximating the projection step may use an iterative procedure) and highly efficient, and it is shown to attain the near-optimal statistical rate of order $\sqrt{(k \log L)/m}$, where $m$ is the number of measurements. We consider two specific instances of the SIM, namely noisy $1$-bit and cubic measurement models, and perform experiments on image datasets to demonstrate the efficacy of our method. In particular, for the noisy $1$-bit measurement model, we show that our non-iterative method significantly outperforms a state-of-the-art iterative method in terms of both accuracy and efficiency.
Generative Principal Component Analysis
Mar 18, 2022
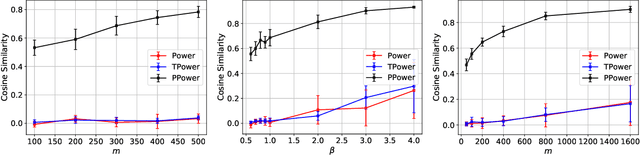


Abstract:In this paper, we study the problem of principal component analysis with generative modeling assumptions, adopting a general model for the observed matrix that encompasses notable special cases, including spiked matrix recovery and phase retrieval. The key assumption is that the underlying signal lies near the range of an $L$-Lipschitz continuous generative model with bounded $k$-dimensional inputs. We propose a quadratic estimator, and show that it enjoys a statistical rate of order $\sqrt{\frac{k\log L}{m}}$, where $m$ is the number of samples. We also provide a near-matching algorithm-independent lower bound. Moreover, we provide a variant of the classic power method, which projects the calculated data onto the range of the generative model during each iteration. We show that under suitable conditions, this method converges exponentially fast to a point achieving the above-mentioned statistical rate. We perform experiments on various image datasets for spiked matrix and phase retrieval models, and illustrate performance gains of our method to the classic power method and the truncated power method devised for sparse principal component analysis.
Rethinking Medical Image Reconstruction via Shape Prior, Going Deeper and Faster: Deep Joint Indirect Registration and Reconstruction
Dec 16, 2019



Abstract:Indirect image registration is a promising technique to improve image reconstruction quality by providing a shape prior for the reconstruction task. In this paper, we propose a novel hybrid method that seeks to reconstruct high quality images from few measurements whilst requiring low computational cost. With this purpose, our framework intertwines indirect registration and reconstruction tasks is a single functional. It is based on two major novelties. Firstly, we introduce a model based on deep nets to solve the indirect registration problem, in which the inversion and registration mappings are recurrently connected through a fixed-point interaction based sparse optimisation. Secondly, we introduce specific inversion blocks, that use the explicit physical forward operator, to map the acquired measurements to the image reconstruction. We also introduce registration blocks based deep nets to predict the registration parameters and warp transformation accurately and efficiently. We demonstrate, through extensive numerical and visual experiments, that our framework outperforms significantly classic reconstruction schemes and other bi-task method; this in terms of both image quality and computational time. Finally, we show generalisation capabilities of our approach by demonstrating their performance on fast Magnetic Resonance Imaging (MRI), sparse view computed tomography (CT) and low dose CT with measurements much below the Nyquist limit.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge