Heuristic Self-Paced Learning for Domain Adaptive Semantic Segmentation under Adverse Conditions

The learning order of semantic classes significantly impacts unsupervised domain adaptation for semantic segmentation, especially under adverse weather conditions. Most existing curricula rely on handcrafted heuristics (e.g., fixed uncertainty metrics) and follow a static schedule, which fails to adapt to a model's evolving, high-dimensional training dynamics, leading to category bias. Inspired by Reinforcement Learning, we cast curriculum learning as a sequential decision problem and propose an autonomous class scheduler. This scheduler consists of two components: (i) a high-dimensional state encoder that maps the model's training status into a latent space and distills key features indicative of progress, and (ii) a category-fair policy-gradient objective that ensures balanced improvement across classes. Coupled with mixed source-target supervision, the learned class rankings direct the network's focus to the most informative classes at each stage, enabling more adaptive and dynamic learning. It is worth noting that our method achieves state-of-the-art performance on three widely used benchmarks (e.g., ACDC, Dark Zurich, and Nighttime Driving) and shows generalization ability in synthetic-to-real semantic segmentation.

Leader and Follower: Interactive Motion Generation under Trajectory Constraints

With the rapid advancement of game and film production, generating interactive motion from texts has garnered significant attention due to its potential to revolutionize content creation processes. In many practical applications, there is a need to impose strict constraints on the motion range or trajectory of virtual characters. However, existing methods that rely solely on textual input face substantial challenges in accurately capturing the user's intent, particularly in specifying the desired trajectory. As a result, the generated motions often lack plausibility and accuracy. Moreover, existing trajectory - based methods for customized motion generation rely on retraining for single - actor scenarios, which limits flexibility and adaptability to different datasets, as well as interactivity in two-actor motions. To generate interactive motion following specified trajectories, this paper decouples complex motion into a Leader - Follower dynamic, inspired by role allocation in partner dancing. Based on this framework, this paper explores the motion range refinement process in interactive motion generation and proposes a training-free approach, integrating a Pace Controller and a Kinematic Synchronization Adapter. The framework enhances the ability of existing models to generate motion that adheres to trajectory by controlling the leader's movement and correcting the follower's motion to align with the leader. Experimental results show that the proposed approach, by better leveraging trajectory information, outperforms existing methods in both realism and accuracy.

Locally Regularized Sparse Graph by Fast Proximal Gradient Descent

Sparse graphs built by sparse representation has been demonstrated to be effective in clustering high-dimensional data. Albeit the compelling empirical performance, the vanilla sparse graph ignores the geometric information of the data by performing sparse representation for each datum separately. In order to obtain a sparse graph aligned with the local geometric structure of data, we propose a novel Support Regularized Sparse Graph, abbreviated as SRSG, for data clustering. SRSG encourages local smoothness on the neighborhoods of nearby data points by a well-defined support regularization term. We propose a fast proximal gradient descent method to solve the non-convex optimization problem of SRSG with the convergence matching the Nesterov's optimal convergence rate of first-order methods on smooth and convex objective function with Lipschitz continuous gradient. Extensive experimental results on various real data sets demonstrate the superiority of SRSG over other competing clustering methods.

Estimation and inference of signals via the stochastic geometry of spectrogram level sets

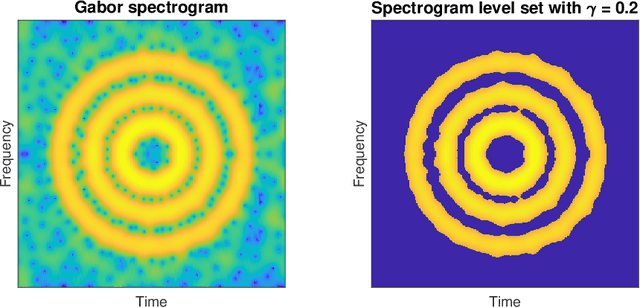
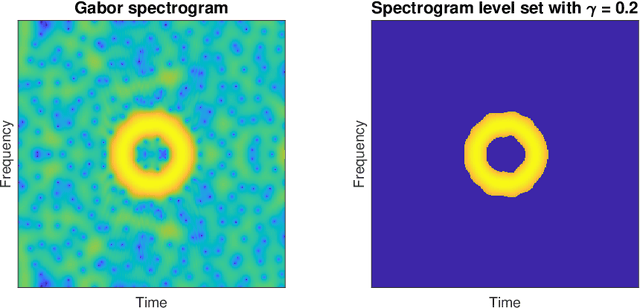
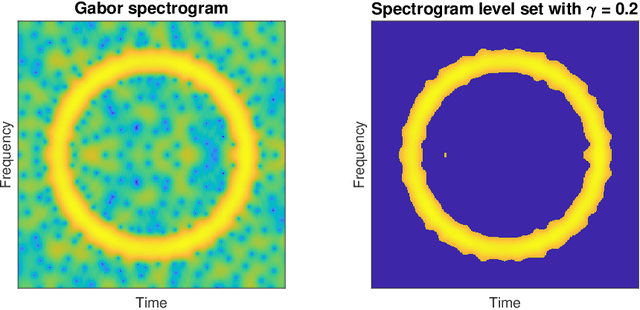
Spectrograms are fundamental tools in the detection, estimation and analysis of signals in the time-frequency analysis paradigm. Signal analysis via spectrograms have traditionally explored their peaks, i.e. their maxima, complemented by a recent interest in their zeros or minima. In particular, recent investigations have demonstrated connections between Gabor spectrograms of Gaussian white noise and Gaussian analytic functions (abbrv. GAFs) in different geometries. However, the zero sets (or the maxima or minima) of GAFs have a complicated stochastic structure, which makes a direct theoretical analysis of usual spectrogram based techniques via GAFs a difficult proposition. These techniques, in turn, largely rely on statistical observables from the analysis of spatial data, whose distributional properties for spectrogram extrema are mostly understood empirically. In this work, we investigate spectrogram analysis via an examination of the stochastic, geometric and analytical properties of their level sets. This includes a comparative analysis of relevant spectrogram structures, with vs without the presence of signals coupled with Gaussian white noise. We obtain theorems demonstrating the efficacy of a spectrogram level sets based approach to the detection and estimation of signals, framed in a concrete inferential set-up. Exploiting these ideas as theoretical underpinnings, we propose a level sets based algorithm for signal analysis that is intrinsic to given spectrogram data. We substantiate the effectiveness of the algorithm by extensive empirical studies, and provide additional theoretical analysis to elucidate some of its key features. Our results also have theoretical implications for spectrogram zero based approaches to signal analysis.