DNNLasso: Scalable Graph Learning for Matrix-Variate Data

We consider the problem of jointly learning row-wise and column-wise dependencies of matrix-variate observations, which are modelled separately by two precision matrices. Due to the complicated structure of Kronecker-product precision matrices in the commonly used matrix-variate Gaussian graphical models, a sparser Kronecker-sum structure was proposed recently based on the Cartesian product of graphs. However, existing methods for estimating Kronecker-sum structured precision matrices do not scale well to large scale datasets. In this paper, we introduce DNNLasso, a diagonally non-negative graphical lasso model for estimating the Kronecker-sum structured precision matrix, which outperforms the state-of-the-art methods by a large margin in both accuracy and computational time. Our code is available at https://github.com/YangjingZhang/DNNLasso.

Learning the hub graphical Lasso model with the structured sparsity via an efficient algorithm

Graphical models have exhibited their performance in numerous tasks ranging from biological analysis to recommender systems. However, graphical models with hub nodes are computationally difficult to fit, particularly when the dimension of the data is large. To efficiently estimate the hub graphical models, we introduce a two-phase algorithm. The proposed algorithm first generates a good initial point via a dual alternating direction method of multipliers (ADMM), and then warm starts a semismooth Newton (SSN) based augmented Lagrangian method (ALM) to compute a solution that is accurate enough for practical tasks. The sparsity structure of the generalized Jacobian ensures that the algorithm can obtain a nice solution very efficiently. Comprehensive experiments on both synthetic data and real data show that it obviously outperforms the existing state-of-the-art algorithms. In particular, in some high dimensional tasks, it can save more than 70\% of the execution time, meanwhile still achieves a high-quality estimation.

Determinantal point processes based on orthogonal polynomials for sampling minibatches in SGD

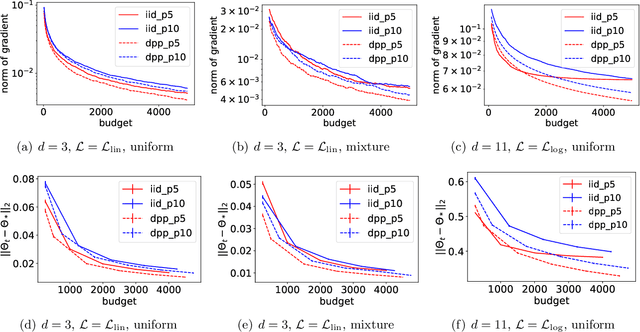
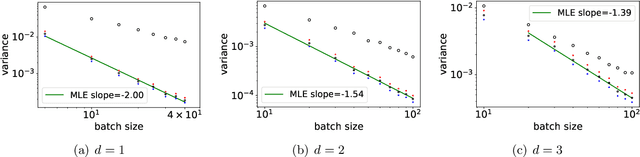
Stochastic gradient descent (SGD) is a cornerstone of machine learning. When the number N of data items is large, SGD relies on constructing an unbiased estimator of the gradient of the empirical risk using a small subset of the original dataset, called a minibatch. Default minibatch construction involves uniformly sampling a subset of the desired size, but alternatives have been explored for variance reduction. In particular, experimental evidence suggests drawing minibatches from determinantal point processes (DPPs), distributions over minibatches that favour diversity among selected items. However, like in recent work on DPPs for coresets, providing a systematic and principled understanding of how and why DPPs help has been difficult. In this work, we contribute an orthogonal polynomial-based DPP paradigm for minibatch sampling in SGD. Our approach leverages the specific data distribution at hand, which endows it with greater sensitivity and power over existing data-agnostic methods. We substantiate our method via a detailed theoretical analysis of its convergence properties, interweaving between the discrete data set and the underlying continuous domain. In particular, we show how specific DPPs and a string of controlled approximations can lead to gradient estimators with a variance that decays faster with the batchsize than under uniform sampling. Coupled with existing finite-time guarantees for SGD on convex objectives, this entails that, DPP minibatches lead to a smaller bound on the mean square approximation error than uniform minibatches. Moreover, our estimators are amenable to a recent algorithm that directly samples linear statistics of DPPs (i.e., the gradient estimator) without sampling the underlying DPP (i.e., the minibatch), thereby reducing computational overhead. We provide detailed synthetic as well as real data experiments to substantiate our theoretical claims.

Estimation and inference of signals via the stochastic geometry of spectrogram level sets

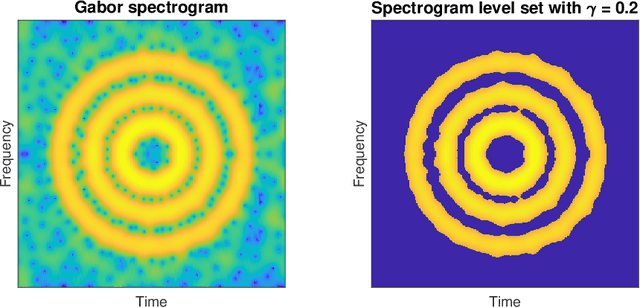
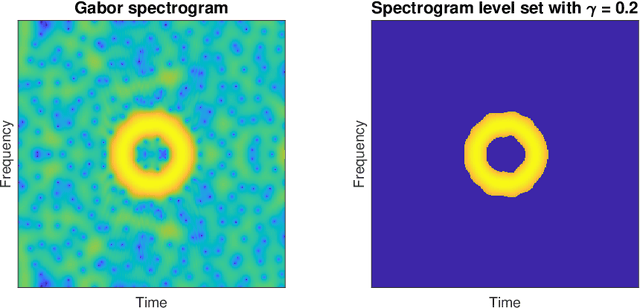
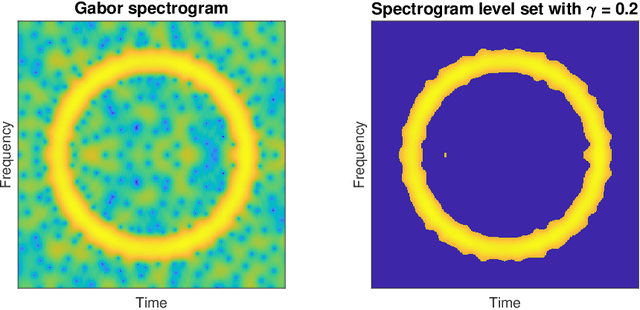
Spectrograms are fundamental tools in the detection, estimation and analysis of signals in the time-frequency analysis paradigm. Signal analysis via spectrograms have traditionally explored their peaks, i.e. their maxima, complemented by a recent interest in their zeros or minima. In particular, recent investigations have demonstrated connections between Gabor spectrograms of Gaussian white noise and Gaussian analytic functions (abbrv. GAFs) in different geometries. However, the zero sets (or the maxima or minima) of GAFs have a complicated stochastic structure, which makes a direct theoretical analysis of usual spectrogram based techniques via GAFs a difficult proposition. These techniques, in turn, largely rely on statistical observables from the analysis of spatial data, whose distributional properties for spectrogram extrema are mostly understood empirically. In this work, we investigate spectrogram analysis via an examination of the stochastic, geometric and analytical properties of their level sets. This includes a comparative analysis of relevant spectrogram structures, with vs without the presence of signals coupled with Gaussian white noise. We obtain theorems demonstrating the efficacy of a spectrogram level sets based approach to the detection and estimation of signals, framed in a concrete inferential set-up. Exploiting these ideas as theoretical underpinnings, we propose a level sets based algorithm for signal analysis that is intrinsic to given spectrogram data. We substantiate the effectiveness of the algorithm by extensive empirical studies, and provide additional theoretical analysis to elucidate some of its key features. Our results also have theoretical implications for spectrogram zero based approaches to signal analysis.

Estimation of sparse Gaussian graphical models with hidden clustering structure

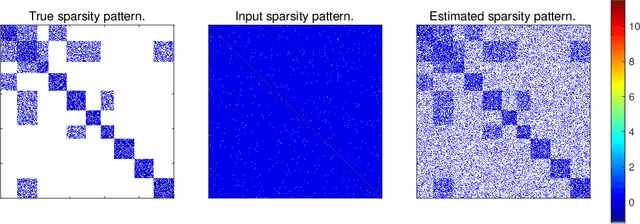
Estimation of Gaussian graphical models is important in natural science when modeling the statistical relationships between variables in the form of a graph. The sparsity and clustering structure of the concentration matrix is enforced to reduce model complexity and describe inherent regularities. We propose a model to estimate the sparse Gaussian graphical models with hidden clustering structure, which also allows additional linear constraints to be imposed on the concentration matrix. We design an efficient two-phase algorithm for solving the proposed model. We develop a symmetric Gauss-Seidel based alternating direction method of the multipliers (sGS-ADMM) to generate an initial point to warm-start the second phase algorithm, which is a proximal augmented Lagrangian method (pALM), to get a solution with high accuracy. Numerical experiments on both synthetic data and real data demonstrate the good performance of our model, as well as the efficiency and robustness of our proposed algorithm.

Efficient algorithms for multivariate shape-constrained convex regression problems

Shape-constrained convex regression problem deals with fitting a convex function to the observed data, where additional constraints are imposed, such as component-wise monotonicity and uniform Lipschitz continuity. This paper provides a comprehensive mechanism for computing the least squares estimator of a multivariate shape-constrained convex regression function in $\mathbb{R}^d$. We prove that the least squares estimator is computable via solving a constrained convex quadratic programming (QP) problem with $(n+1)d$ variables and at least $n(n-1)$ linear inequality constraints, where $n$ is the number of data points. For solving the generally very large-scale convex QP, we design two efficient algorithms, one is the symmetric Gauss-Seidel based alternating direction method of multipliers ({\tt sGS-ADMM}), and the other is the proximal augmented Lagrangian method ({\tt pALM}) with the subproblems solved by the semismooth Newton method ({\tt SSN}). Comprehensive numerical experiments, including those in the pricing of basket options and estimation of production functions in economics, demonstrate that both of our proposed algorithms outperform the state-of-the-art algorithm. The {\tt pALM} is more efficient than the {\tt sGS-ADMM} but the latter has the advantage of being simpler to implement.

On the Closed-form Proximal Mapping and Efficient Algorithms for Exclusive Lasso Models

The exclusive lasso regularization based on the $\ell_{1,2}$ norm has become popular recently due to its superior performance over the group lasso regularization. Comparing to the group lasso regularization which enforces the competition on variables among different groups and results in inter-group sparsity, the exclusive lasso regularization also enforces the competition within each group and results in intra-group sparsity. However, to the best of our knowledge, a correct closed-form solution to the proximal mapping of the $\ell_{1,2}$ norm has still been elusive. In this paper, we fill the gap by deriving a closed-form solution for $\rm{Prox}_{\rho\|\cdot\|_1^2}(\cdot)$ and its generalized Jacobian. Based on the obtained analytical results, we are able to design efficient first and second order algorithms for machine learning models involving the exclusive lasso regularization. Our analytical solution of the proximal mapping for the exclusive lasso regularization can be used to improve the efficiency of existing algorithms relying on the efficient computation of the proximal mapping.

Efficient sparse Hessian based algorithms for the clustered lasso problem

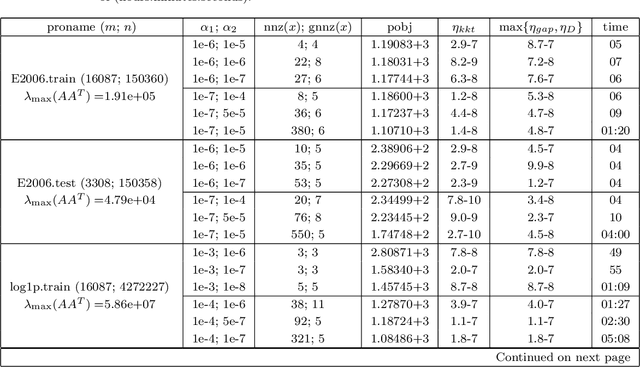
We focus on solving the clustered lasso problem, which is a least squares problem with the $\ell_1$-type penalties imposed on both the coefficients and their pairwise differences to learn the group structure of the regression parameters. Here we first reformulate the clustered lasso regularizer as a weighted ordered-lasso regularizer, which is essential in reducing the computational cost from $O(n^2)$ to $O(n\log (n))$. We then propose an inexact semismooth Newton augmented Lagrangian (SSNAL) algorithm to solve the clustered lasso problem or its dual via this equivalent formulation, depending on whether the sample size is larger than the dimension of the features. An essential component of the SSNAL algorithm is the computation of the generalized Jacobian of the proximal mapping of the clustered lasso regularizer. Based on the new formulation, we derive an efficient procedure for its computation. Comprehensive results on the global convergence and local linear convergence of the SSNAL algorithm are established. For the purpose of exposition and comparison, we also summarize/design several first-order methods that can be used to solve the problem under consideration, but with the key improvement from the new formulation of the clustered lasso regularizer. As a demonstration of the applicability of our algorithms, numerical experiments on the clustered lasso problem are performed. The experiments show that the SSNAL algorithm substantially outperforms the best alternative algorithm for the clustered lasso problem.