Negative Dependence as a toolbox for machine learning : review and new developments

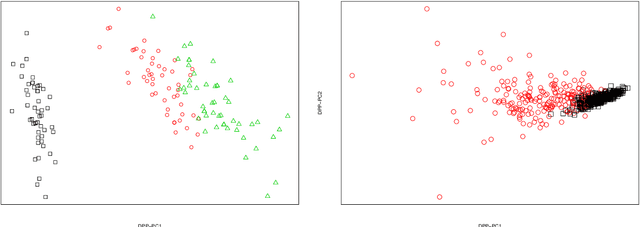
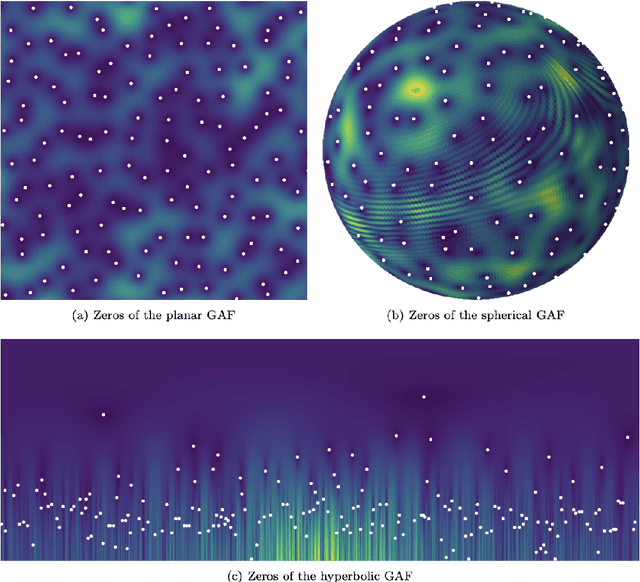
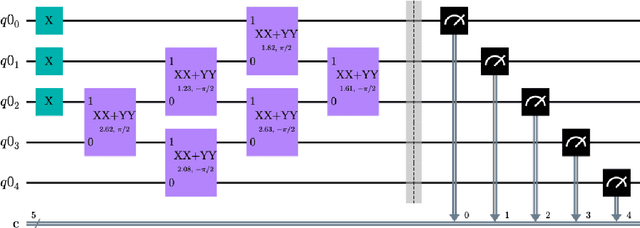
Negative dependence is becoming a key driver in advancing learning capabilities beyond the limits of traditional independence. Recent developments have evidenced support towards negatively dependent systems as a learning paradigm in a broad range of fundamental machine learning challenges including optimization, sampling, dimensionality reduction and sparse signal recovery, often surpassing the performance of current methods based on statistical independence. The most popular negatively dependent model has been that of determinantal point processes (DPPs), which have their origins in quantum theory. However, other models, such as perturbed lattice models, strongly Rayleigh measures, zeros of random functions have gained salience in various learning applications. In this article, we review this burgeoning field of research, as it has developed over the past two decades or so. We also present new results on applications of DPPs to the parsimonious representation of neural networks. In the limited scope of the article, we mostly focus on aspects of this area to which the authors contributed over the recent years, including applications to Monte Carlo methods, coresets and stochastic gradient descent, stochastic networks, signal processing and connections to quantum computation. However, starting from basics of negative dependence for the uninitiated reader, extensive references are provided to a broad swath of related developments which could not be covered within our limited scope. While existing works and reviews generally focus on specific negatively dependent models (e.g. DPPs), a notable feature of this article is that it addresses negative dependence as a machine learning methodology as a whole. In this vein, it covers within its span an array of negatively dependent models and their applications well beyond DPPs, thereby putting forward a very general and rather unique perspective.

Determinantal point processes based on orthogonal polynomials for sampling minibatches in SGD

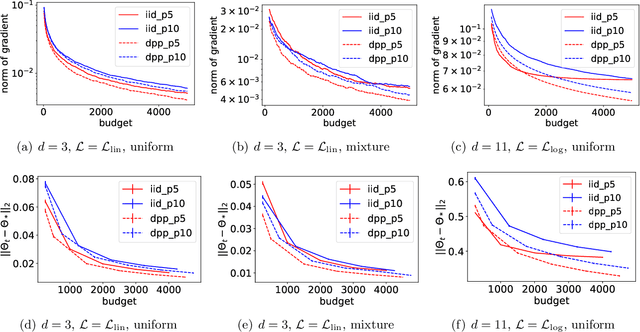
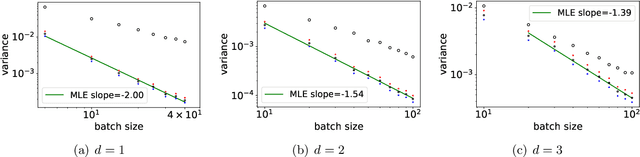
Stochastic gradient descent (SGD) is a cornerstone of machine learning. When the number N of data items is large, SGD relies on constructing an unbiased estimator of the gradient of the empirical risk using a small subset of the original dataset, called a minibatch. Default minibatch construction involves uniformly sampling a subset of the desired size, but alternatives have been explored for variance reduction. In particular, experimental evidence suggests drawing minibatches from determinantal point processes (DPPs), distributions over minibatches that favour diversity among selected items. However, like in recent work on DPPs for coresets, providing a systematic and principled understanding of how and why DPPs help has been difficult. In this work, we contribute an orthogonal polynomial-based DPP paradigm for minibatch sampling in SGD. Our approach leverages the specific data distribution at hand, which endows it with greater sensitivity and power over existing data-agnostic methods. We substantiate our method via a detailed theoretical analysis of its convergence properties, interweaving between the discrete data set and the underlying continuous domain. In particular, we show how specific DPPs and a string of controlled approximations can lead to gradient estimators with a variance that decays faster with the batchsize than under uniform sampling. Coupled with existing finite-time guarantees for SGD on convex objectives, this entails that, DPP minibatches lead to a smaller bound on the mean square approximation error than uniform minibatches. Moreover, our estimators are amenable to a recent algorithm that directly samples linear statistics of DPPs (i.e., the gradient estimator) without sampling the underlying DPP (i.e., the minibatch), thereby reducing computational overhead. We provide detailed synthetic as well as real data experiments to substantiate our theoretical claims.