Learning Gaussian Graphical Models with Observed or Latent FVSs

Gaussian Graphical Models (GGMs) or Gauss Markov random fields are widely used in many applications, and the trade-off between the modeling capacity and the efficiency of learning and inference has been an important research problem. In this paper, we study the family of GGMs with small feedback vertex sets (FVSs), where an FVS is a set of nodes whose removal breaks all the cycles. Exact inference such as computing the marginal distributions and the partition function has complexity $O(k^{2}n)$ using message-passing algorithms, where k is the size of the FVS, and n is the total number of nodes. We propose efficient structure learning algorithms for two cases: 1) All nodes are observed, which is useful in modeling social or flight networks where the FVS nodes often correspond to a small number of high-degree nodes, or hubs, while the rest of the networks is modeled by a tree. Regardless of the maximum degree, without knowing the full graph structure, we can exactly compute the maximum likelihood estimate in $O(kn^2+n^2\log n)$ if the FVS is known or in polynomial time if the FVS is unknown but has bounded size. 2) The FVS nodes are latent variables, where structure learning is equivalent to decomposing a inverse covariance matrix (exactly or approximately) into the sum of a tree-structured matrix and a low-rank matrix. By incorporating efficient inference into the learning steps, we can obtain a learning algorithm using alternating low-rank correction with complexity $O(kn^{2}+n^{2}\log n)$ per iteration. We also perform experiments using both synthetic data as well as real data of flight delays to demonstrate the modeling capacity with FVSs of various sizes.

Rejoinder: Latent variable graphical model selection via convex optimization

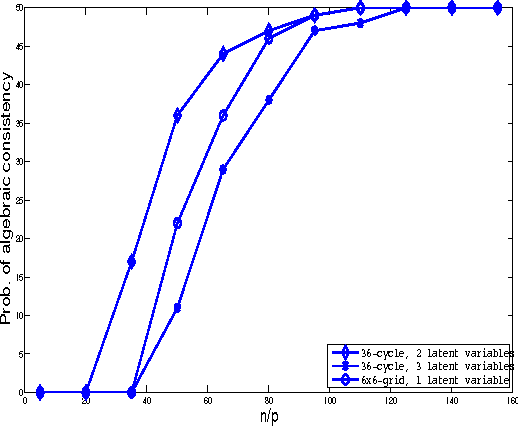
Rejoinder to "Latent variable graphical model selection via convex optimization" by Venkat Chandrasekaran, Pablo A. Parrilo and Alan S. Willsky [arXiv:1008.1290].

Bayesian Nonparametric Hidden Semi-Markov Models

There is much interest in the Hierarchical Dirichlet Process Hidden Markov Model (HDP-HMM) as a natural Bayesian nonparametric extension of the ubiquitous Hidden Markov Model for learning from sequential and time-series data. However, in many settings the HDP-HMM's strict Markovian constraints are undesirable, particularly if we wish to learn or encode non-geometric state durations. We can extend the HDP-HMM to capture such structure by drawing upon explicit-duration semi-Markovianity, which has been developed mainly in the parametric frequentist setting, to allow construction of highly interpretable models that admit natural prior information on state durations. In this paper we introduce the explicit-duration Hierarchical Dirichlet Process Hidden semi-Markov Model (HDP-HSMM) and develop sampling algorithms for efficient posterior inference. The methods we introduce also provide new methods for sampling inference in the finite Bayesian HSMM. Our modular Gibbs sampling methods can be embedded in samplers for larger hierarchical Bayesian models, adding semi-Markov chain modeling as another tool in the Bayesian inference toolbox. We demonstrate the utility of the HDP-HSMM and our inference methods on both synthetic and real experiments.

High-dimensional structure estimation in Ising models: Local separation criterion

We consider the problem of high-dimensional Ising (graphical) model selection. We propose a simple algorithm for structure estimation based on the thresholding of the empirical conditional variation distances. We introduce a novel criterion for tractable graph families, where this method is efficient, based on the presence of sparse local separators between node pairs in the underlying graph. For such graphs, the proposed algorithm has a sample complexity of $n=\Omega(J_{\min}^{-2}\log p)$, where $p$ is the number of variables, and $J_{\min}$ is the minimum (absolute) edge potential in the model. We also establish nonasymptotic necessary and sufficient conditions for structure estimation.

Joint Modeling of Multiple Related Time Series via the Beta Process

We propose a Bayesian nonparametric approach to the problem of jointly modeling multiple related time series. Our approach is based on the discovery of a set of latent, shared dynamical behaviors. Using a beta process prior, the size of the set and the sharing pattern are both inferred from data. We develop efficient Markov chain Monte Carlo methods based on the Indian buffet process representation of the predictive distribution of the beta process, without relying on a truncated model. In particular, our approach uses the sum-product algorithm to efficiently compute Metropolis-Hastings acceptance probabilities, and explores new dynamical behaviors via birth and death proposals. We examine the benefits of our proposed feature-based model on several synthetic datasets, and also demonstrate promising results on unsupervised segmentation of visual motion capture data.

A sticky HDP-HMM with application to speaker diarization

We consider the problem of speaker diarization, the problem of segmenting an audio recording of a meeting into temporal segments corresponding to individual speakers. The problem is rendered particularly difficult by the fact that we are not allowed to assume knowledge of the number of people participating in the meeting. To address this problem, we take a Bayesian nonparametric approach to speaker diarization that builds on the hierarchical Dirichlet process hidden Markov model (HDP-HMM) of Teh et al. [J. Amer. Statist. Assoc. 101 (2006) 1566--1581]. Although the basic HDP-HMM tends to over-segment the audio data---creating redundant states and rapidly switching among them---we describe an augmented HDP-HMM that provides effective control over the switching rate. We also show that this augmentation makes it possible to treat emission distributions nonparametrically. To scale the resulting architecture to realistic diarization problems, we develop a sampling algorithm that employs a truncated approximation of the Dirichlet process to jointly resample the full state sequence, greatly improving mixing rates. Working with a benchmark NIST data set, we show that our Bayesian nonparametric architecture yields state-of-the-art speaker diarization results.

Feedback Message Passing for Inference in Gaussian Graphical Models

While loopy belief propagation (LBP) performs reasonably well for inference in some Gaussian graphical models with cycles, its performance is unsatisfactory for many others. In particular for some models LBP does not converge, and in general when it does converge, the computed variances are incorrect (except for cycle-free graphs for which belief propagation (BP) is non-iterative and exact). In this paper we propose {\em feedback message passing} (FMP), a message-passing algorithm that makes use of a special set of vertices (called a {\em feedback vertex set} or {\em FVS}) whose removal results in a cycle-free graph. In FMP, standard BP is employed several times on the cycle-free subgraph excluding the FVS while a special message-passing scheme is used for the nodes in the FVS. The computational complexity of exact inference is $O(k^2n)$, where $k$ is the number of feedback nodes, and $n$ is the total number of nodes. When the size of the FVS is very large, FMP is intractable. Hence we propose {\em approximate FMP}, where a pseudo-FVS is used instead of an FVS, and where inference in the non-cycle-free graph obtained by removing the pseudo-FVS is carried out approximately using LBP. We show that, when approximate FMP converges, it yields exact means and variances on the pseudo-FVS and exact means throughout the remainder of the graph. We also provide theoretical results on the convergence and accuracy of approximate FMP. In particular, we prove error bounds on variance computation. Based on these theoretical results, we design efficient algorithms to select a pseudo-FVS of bounded size. The choice of the pseudo-FVS allows us to explicitly trade off between efficiency and accuracy. Experimental results show that using a pseudo-FVS of size no larger than $\log(n)$, this procedure converges much more often, more quickly, and provides more accurate results than LBP on the entire graph.

Learning High-Dimensional Markov Forest Distributions: Analysis of Error Rates

The problem of learning forest-structured discrete graphical models from i.i.d. samples is considered. An algorithm based on pruning of the Chow-Liu tree through adaptive thresholding is proposed. It is shown that this algorithm is both structurally consistent and risk consistent and the error probability of structure learning decays faster than any polynomial in the number of samples under fixed model size. For the high-dimensional scenario where the size of the model d and the number of edges k scale with the number of samples n, sufficient conditions on (n,d,k) are given for the algorithm to satisfy structural and risk consistencies. In addition, the extremal structures for learning are identified; we prove that the independent (resp. tree) model is the hardest (resp. easiest) to learn using the proposed algorithm in terms of error rates for structure learning.

A Large-Deviation Analysis of the Maximum-Likelihood Learning of Markov Tree Structures

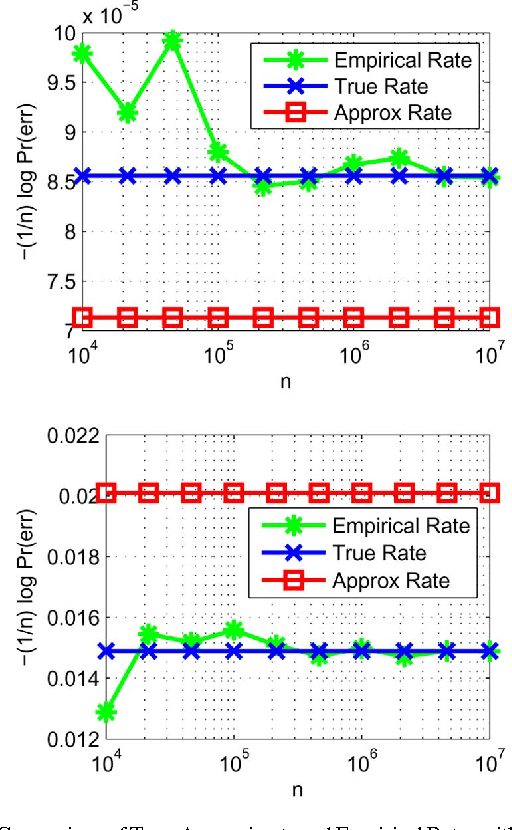
The problem of maximum-likelihood (ML) estimation of discrete tree-structured distributions is considered. Chow and Liu established that ML-estimation reduces to the construction of a maximum-weight spanning tree using the empirical mutual information quantities as the edge weights. Using the theory of large-deviations, we analyze the exponent associated with the error probability of the event that the ML-estimate of the Markov tree structure differs from the true tree structure, given a set of independently drawn samples. By exploiting the fact that the output of ML-estimation is a tree, we establish that the error exponent is equal to the exponential rate of decay of a single dominant crossover event. We prove that in this dominant crossover event, a non-neighbor node pair replaces a true edge of the distribution that is along the path of edges in the true tree graph connecting the nodes in the non-neighbor pair. Using ideas from Euclidean information theory, we then analyze the scenario of ML-estimation in the very noisy learning regime and show that the error exponent can be approximated as a ratio, which is interpreted as the signal-to-noise ratio (SNR) for learning tree distributions. We show via numerical experiments that in this regime, our SNR approximation is accurate.

Learning Latent Tree Graphical Models

We study the problem of learning a latent tree graphical model where samples are available only from a subset of variables. We propose two consistent and computationally efficient algorithms for learning minimal latent trees, that is, trees without any redundant hidden nodes. Unlike many existing methods, the observed nodes (or variables) are not constrained to be leaf nodes. Our first algorithm, recursive grouping, builds the latent tree recursively by identifying sibling groups using so-called information distances. One of the main contributions of this work is our second algorithm, which we refer to as CLGrouping. CLGrouping starts with a pre-processing procedure in which a tree over the observed variables is constructed. This global step groups the observed nodes that are likely to be close to each other in the true latent tree, thereby guiding subsequent recursive grouping (or equivalent procedures) on much smaller subsets of variables. This results in more accurate and efficient learning of latent trees. We also present regularized versions of our algorithms that learn latent tree approximations of arbitrary distributions. We compare the proposed algorithms to other methods by performing extensive numerical experiments on various latent tree graphical models such as hidden Markov models and star graphs. In addition, we demonstrate the applicability of our methods on real-world datasets by modeling the dependency structure of monthly stock returns in the S&P index and of the words in the 20 newsgroups dataset.