A Large-Deviation Analysis of the Maximum-Likelihood Learning of Markov Tree Structures
Paper and Code
Nov 21, 2010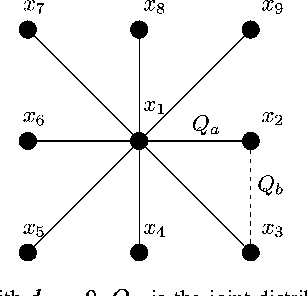


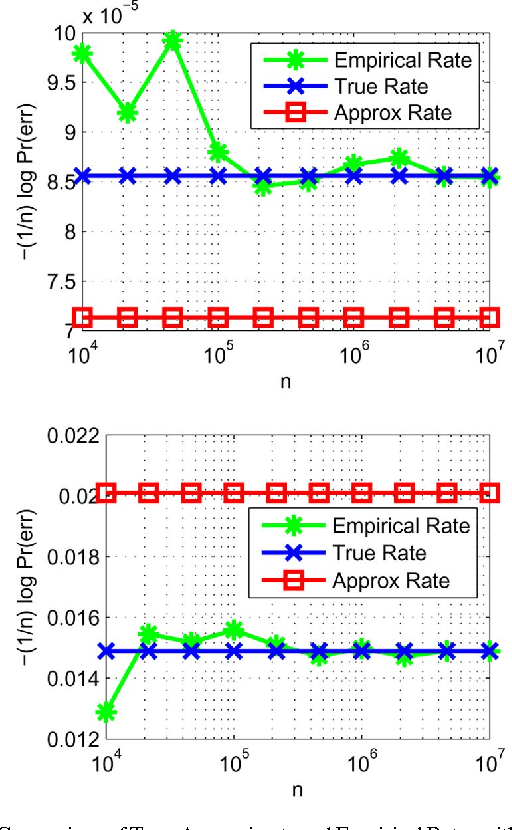
The problem of maximum-likelihood (ML) estimation of discrete tree-structured distributions is considered. Chow and Liu established that ML-estimation reduces to the construction of a maximum-weight spanning tree using the empirical mutual information quantities as the edge weights. Using the theory of large-deviations, we analyze the exponent associated with the error probability of the event that the ML-estimate of the Markov tree structure differs from the true tree structure, given a set of independently drawn samples. By exploiting the fact that the output of ML-estimation is a tree, we establish that the error exponent is equal to the exponential rate of decay of a single dominant crossover event. We prove that in this dominant crossover event, a non-neighbor node pair replaces a true edge of the distribution that is along the path of edges in the true tree graph connecting the nodes in the non-neighbor pair. Using ideas from Euclidean information theory, we then analyze the scenario of ML-estimation in the very noisy learning regime and show that the error exponent can be approximated as a ratio, which is interpreted as the signal-to-noise ratio (SNR) for learning tree distributions. We show via numerical experiments that in this regime, our SNR approximation is accurate.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge