An Invariance Principle for Polytopes

Let X be randomly chosen from {-1,1}^n, and let Y be randomly chosen from the standard spherical Gaussian on R^n. For any (possibly unbounded) polytope P formed by the intersection of k halfspaces, we prove that |Pr [X belongs to P] - Pr [Y belongs to P]| < log^{8/5}k * Delta, where Delta is a parameter that is small for polytopes formed by the intersection of "regular" halfspaces (i.e., halfspaces with low influence). The novelty of our invariance principle is the polylogarithmic dependence on k. Previously, only bounds that were at least linear in k were known. We give two important applications of our main result: (1) A polylogarithmic in k bound on the Boolean noise sensitivity of intersections of k "regular" halfspaces (previous work gave bounds linear in k). (2) A pseudorandom generator (PRG) with seed length O((log n)*poly(log k,1/delta)) that delta-fools all polytopes with k faces with respect to the Gaussian distribution. We also obtain PRGs with similar parameters that fool polytopes formed by intersection of regular halfspaces over the hypercube. Using our PRG constructions, we obtain the first deterministic quasi-polynomial time algorithms for approximately counting the number of solutions to a broad class of integer programs, including dense covering problems and contingency tables.

Complexity of Inference in Graphical Models

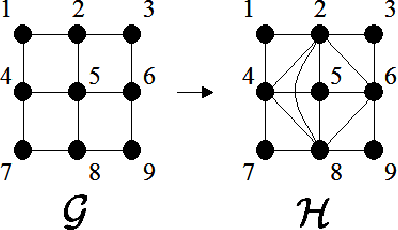
It is well-known that inference in graphical models is hard in the worst case, but tractable for models with bounded treewidth. We ask whether treewidth is the only structural criterion of the underlying graph that enables tractable inference. In other words, is there some class of structures with unbounded treewidth in which inference is tractable? Subject to a combinatorial hypothesis due to Robertson et al. (1994), we show that low treewidth is indeed the only structural restriction that can ensure tractability. Thus, even for the "best case" graph structure, there is no inference algorithm with complexity polynomial in the treewidth.

Bounding the Sensitivity of Polynomial Threshold Functions

We give the first non-trivial upper bounds on the average sensitivity and noise sensitivity of polynomial threshold functions. More specifically, for a Boolean function f on n variables equal to the sign of a real, multivariate polynomial of total degree d we prove 1) The average sensitivity of f is at most O(n^{1-1/(4d+6)}) (we also give a combinatorial proof of the bound O(n^{1-1/2^d}). 2) The noise sensitivity of f with noise rate \delta is at most O(\delta^{1/(4d+6)}). Previously, only bounds for the linear case were known. Along the way we show new structural theorems about random restrictions of polynomial threshold functions obtained via hypercontractivity. These structural results may be of independent interest as they provide a generic template for transforming problems related to polynomial threshold functions defined on the Boolean hypercube to polynomial threshold functions defined in Gaussian space.