Amine Bennouna
What Data Enables Optimal Decisions? An Exact Characterization for Linear Optimization
May 27, 2025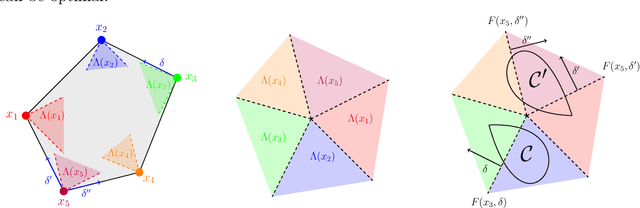
Abstract:We study the fundamental question of how informative a dataset is for solving a given decision-making task. In our setting, the dataset provides partial information about unknown parameters that influence task outcomes. Focusing on linear programs, we characterize when a dataset is sufficient to recover an optimal decision, given an uncertainty set on the cost vector. Our main contribution is a sharp geometric characterization that identifies the directions of the cost vector that matter for optimality, relative to the task constraints and uncertainty set. We further develop a practical algorithm that, for a given task, constructs a minimal or least-costly sufficient dataset. Our results reveal that small, well-chosen datasets can often fully determine optimal decisions -- offering a principled foundation for task-aware data selection.
From Distributional Robustness to Robust Statistics: A Confidence Sets Perspective
Oct 17, 2024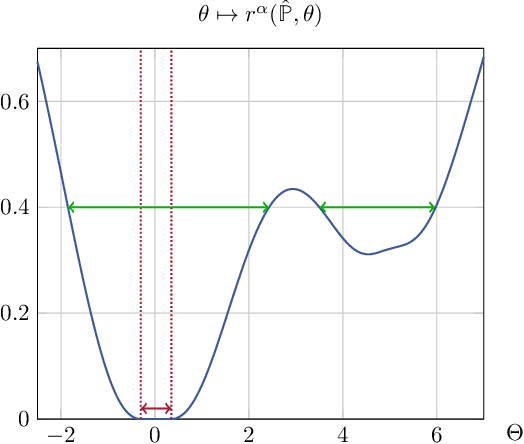
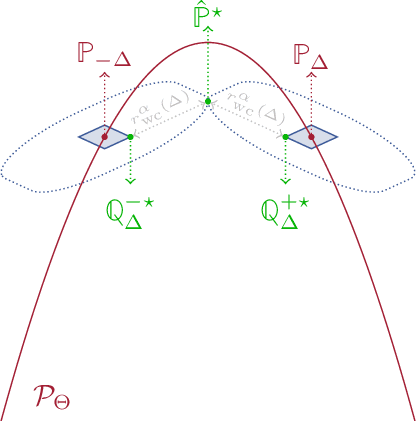
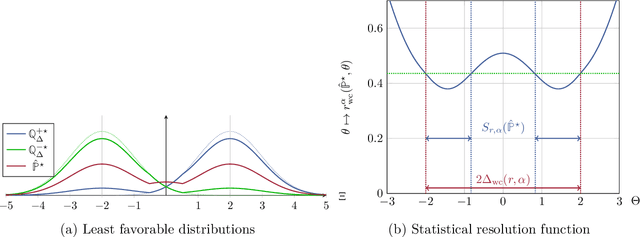
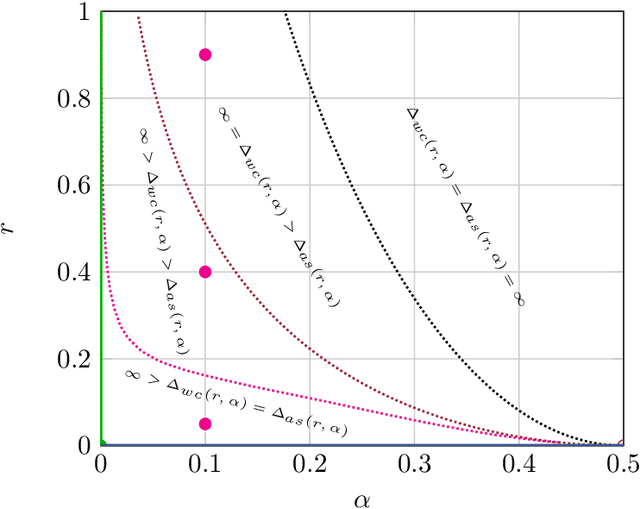
Abstract:We establish a connection between distributionally robust optimization (DRO) and classical robust statistics. We demonstrate that this connection arises naturally in the context of estimation under data corruption, where the goal is to construct ``minimal'' confidence sets for the unknown data-generating distribution. Specifically, we show that a DRO ambiguity set, based on the Kullback-Leibler divergence and total variation distance, is uniformly minimal, meaning it represents the smallest confidence set that contains the unknown distribution with at a given confidence power. Moreover, we prove that when parametric assumptions are imposed on the unknown distribution, the ambiguity set is never larger than a confidence set based on the optimal estimator proposed by Huber. This insight reveals that the commonly observed conservatism of DRO formulations is not intrinsic to these formulations themselves but rather stems from the non-parametric framework in which these formulations are employed.
Certified Robust Neural Networks: Generalization and Corruption Resistance
Mar 03, 2023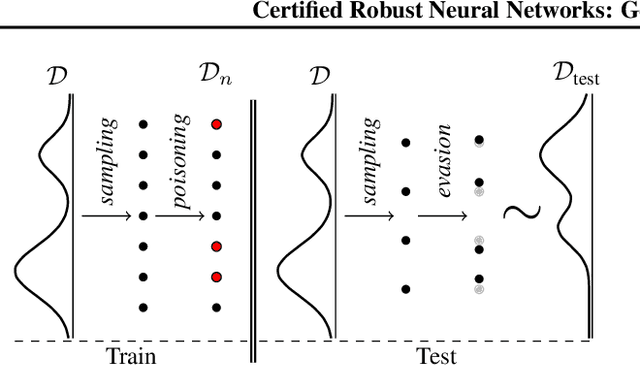


Abstract:Adversarial training aims to reduce the problematic susceptibility of modern neural networks to small data perturbations. Surprisingly, overfitting is a major concern in adversarial training of neural networks despite being mostly absent in standard training. We provide here theoretical evidence for this peculiar ``robust overfitting'' phenomenon. Subsequently, we advance a novel loss function which we show both theoretically as well as empirically to enjoy a certified level of robustness against data evasion and poisoning attacks while ensuring guaranteed generalization. We indicate through careful numerical experiments that our resulting holistic robust (HR) training procedure yields SOTA performance in terms of adversarial error loss. Finally, we indicate that HR training can be interpreted as a direct extension of adversarial training and comes with a negligible additional computational burden.
Holistic Robust Data-Driven Decisions
Jul 19, 2022



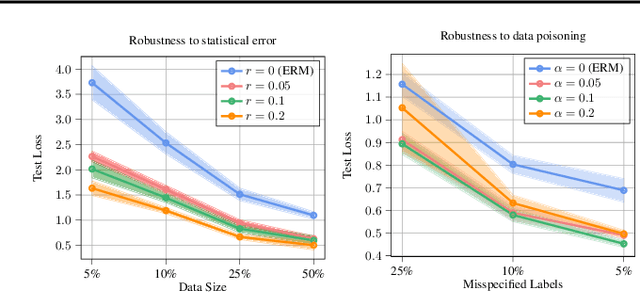
Abstract:The design of data-driven formulations for machine learning and decision-making with good out-of-sample performance is a key challenge. The observation that good in-sample performance does not guarantee good out-of-sample performance is generally known as overfitting. Practical overfitting can typically not be attributed to a single cause but instead is caused by several factors all at once. We consider here three overfitting sources: (i) statistical error as a result of working with finite sample data, (ii) data noise which occurs when the data points are measured only with finite precision, and finally (iii) data misspecification in which a small fraction of all data may be wholly corrupted. We argue that although existing data-driven formulations may be robust against one of these three sources in isolation they do not provide holistic protection against all overfitting sources simultaneously. We design a novel data-driven formulation which does guarantee such holistic protection and is furthermore computationally viable. Our distributionally robust optimization formulation can be interpreted as a novel combination of a Kullback-Leibler and Levy-Prokhorov robust optimization formulation. Finally, we show how in the context of classification and regression problems several popular regularized and robust formulations reduce to a particular case of our proposed more general formulation.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge