From Distributional Robustness to Robust Statistics: A Confidence Sets Perspective
Paper and Code
Oct 17, 2024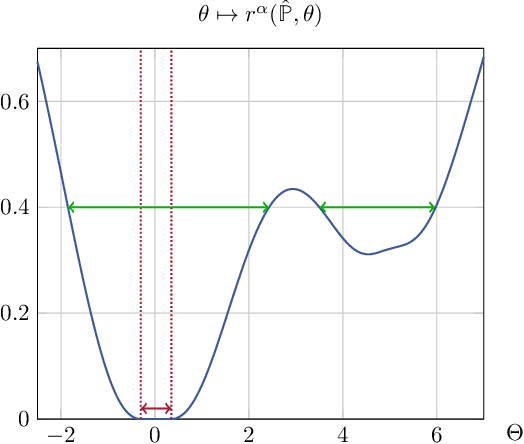
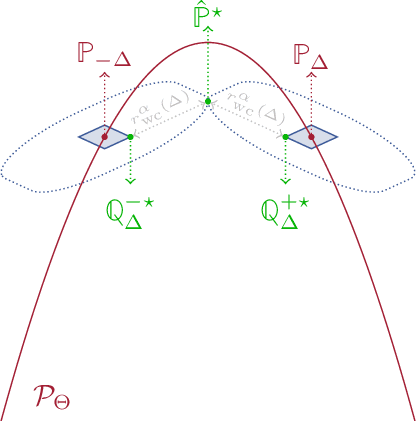
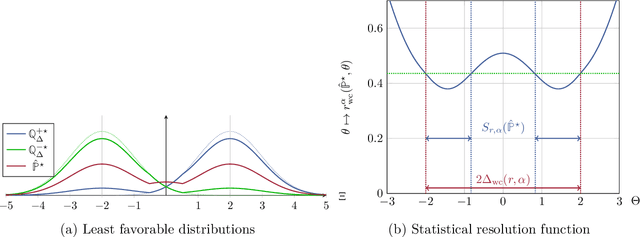
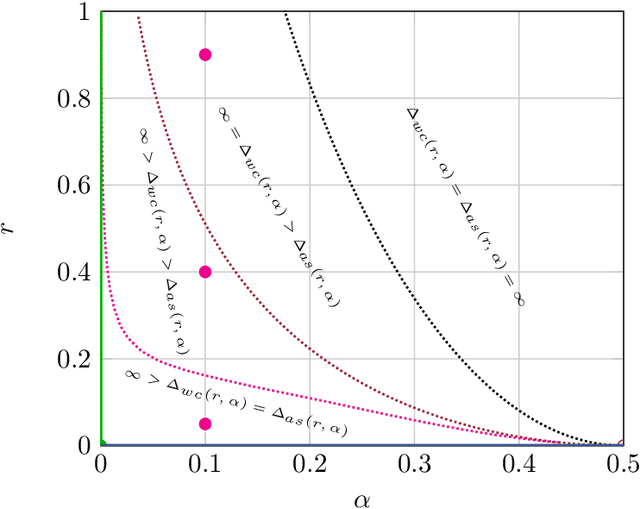
We establish a connection between distributionally robust optimization (DRO) and classical robust statistics. We demonstrate that this connection arises naturally in the context of estimation under data corruption, where the goal is to construct ``minimal'' confidence sets for the unknown data-generating distribution. Specifically, we show that a DRO ambiguity set, based on the Kullback-Leibler divergence and total variation distance, is uniformly minimal, meaning it represents the smallest confidence set that contains the unknown distribution with at a given confidence power. Moreover, we prove that when parametric assumptions are imposed on the unknown distribution, the ambiguity set is never larger than a confidence set based on the optimal estimator proposed by Huber. This insight reveals that the commonly observed conservatism of DRO formulations is not intrinsic to these formulations themselves but rather stems from the non-parametric framework in which these formulations are employed.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge