From Distributional Robustness to Robust Statistics: A Confidence Sets Perspective

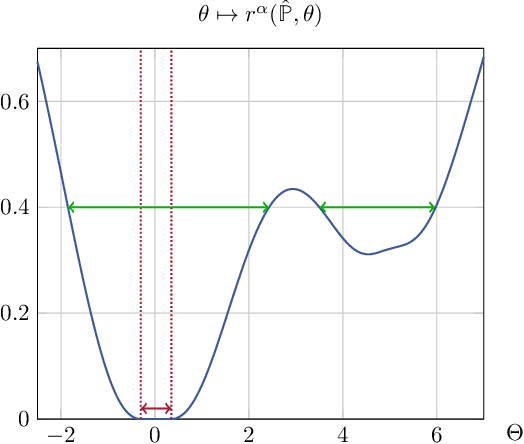
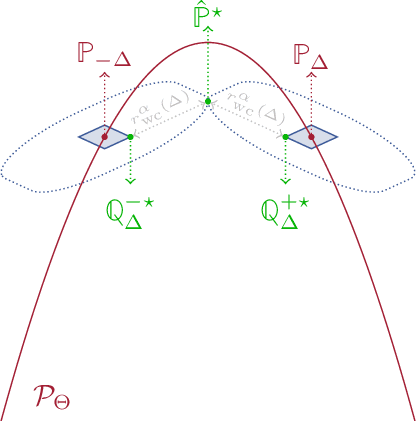
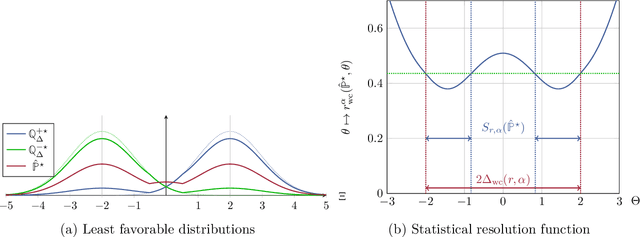
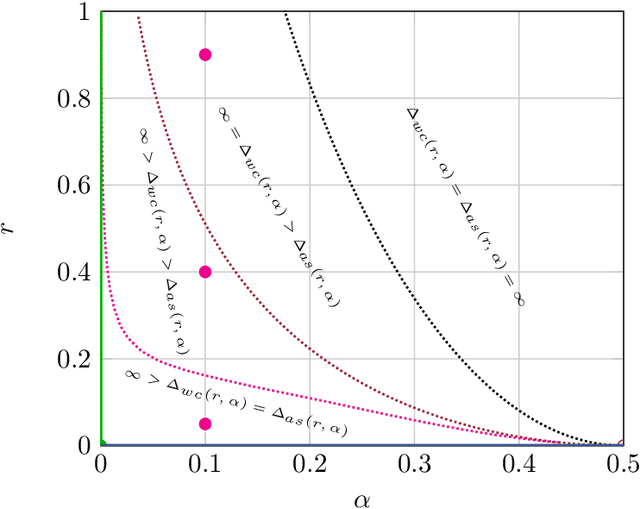
We establish a connection between distributionally robust optimization (DRO) and classical robust statistics. We demonstrate that this connection arises naturally in the context of estimation under data corruption, where the goal is to construct ``minimal'' confidence sets for the unknown data-generating distribution. Specifically, we show that a DRO ambiguity set, based on the Kullback-Leibler divergence and total variation distance, is uniformly minimal, meaning it represents the smallest confidence set that contains the unknown distribution with at a given confidence power. Moreover, we prove that when parametric assumptions are imposed on the unknown distribution, the ambiguity set is never larger than a confidence set based on the optimal estimator proposed by Huber. This insight reveals that the commonly observed conservatism of DRO formulations is not intrinsic to these formulations themselves but rather stems from the non-parametric framework in which these formulations are employed.

Certified Robust Neural Networks: Generalization and Corruption Resistance

Adversarial training aims to reduce the problematic susceptibility of modern neural networks to small data perturbations. Surprisingly, overfitting is a major concern in adversarial training of neural networks despite being mostly absent in standard training. We provide here theoretical evidence for this peculiar ``robust overfitting'' phenomenon. Subsequently, we advance a novel loss function which we show both theoretically as well as empirically to enjoy a certified level of robustness against data evasion and poisoning attacks while ensuring guaranteed generalization. We indicate through careful numerical experiments that our resulting holistic robust (HR) training procedure yields SOTA performance in terms of adversarial error loss. Finally, we indicate that HR training can be interpreted as a direct extension of adversarial training and comes with a negligible additional computational burden.

Holistic Robust Data-Driven Decisions

The design of data-driven formulations for machine learning and decision-making with good out-of-sample performance is a key challenge. The observation that good in-sample performance does not guarantee good out-of-sample performance is generally known as overfitting. Practical overfitting can typically not be attributed to a single cause but instead is caused by several factors all at once. We consider here three overfitting sources: (i) statistical error as a result of working with finite sample data, (ii) data noise which occurs when the data points are measured only with finite precision, and finally (iii) data misspecification in which a small fraction of all data may be wholly corrupted. We argue that although existing data-driven formulations may be robust against one of these three sources in isolation they do not provide holistic protection against all overfitting sources simultaneously. We design a novel data-driven formulation which does guarantee such holistic protection and is furthermore computationally viable. Our distributionally robust optimization formulation can be interpreted as a novel combination of a Kullback-Leibler and Levy-Prokhorov robust optimization formulation. Finally, we show how in the context of classification and regression problems several popular regularized and robust formulations reduce to a particular case of our proposed more general formulation.

Bootstrap Robust Prescriptive Analytics

We address the problem of prescribing an optimal decision in a framework where its cost depends on uncertain problem parameters $Y$ that need to be learned from data. Earlier work by Bertsimas and Kallus (2014) transforms classical machine learning methods that merely predict $Y$ from supervised training data $[(x_1, y_1), \dots, (x_n, y_n)]$ into prescriptive methods taking optimal decisions specific to a particular covariate context $X=\bar x$. Their prescriptive methods factor in additional observed contextual information on a potentially large number of covariates $X=\bar x$ to take context specific actions $z(\bar x)$ which are superior to any static decision $z$. Any naive use of limited training data may, however, lead to gullible decisions over-calibrated to one particular data set. In this paper, we borrow ideas from distributionally robust optimization and the statistical bootstrap of Efron (1982) to propose two novel prescriptive methods based on (nw) Nadaraya-Watson and (nn) nearest-neighbors learning which safeguard against overfitting and lead to improved out-of-sample performance. Both resulting robust prescriptive methods reduce to tractable convex optimization problems and enjoy a limited disappointment on bootstrap data. We illustrate the data-driven decision-making framework and our novel robustness notion on a small news vendor problem as well as a small portfolio allocation problem.

Sparse Hierarchical Regression with Polynomials

We present a novel method for exact hierarchical sparse polynomial regression. Our regressor is that degree $r$ polynomial which depends on at most $k$ inputs, counting at most $\ell$ monomial terms, which minimizes the sum of the squares of its prediction errors. The previous hierarchical sparse specification aligns well with modern big data settings where many inputs are not relevant for prediction purposes and the functional complexity of the regressor needs to be controlled as to avoid overfitting. We present a two-step approach to this hierarchical sparse regression problem. First, we discard irrelevant inputs using an extremely fast input ranking heuristic. Secondly, we take advantage of modern cutting plane methods for integer optimization to solve our resulting reduced hierarchical $(k, \ell)$-sparse problem exactly. The ability of our method to identify all $k$ relevant inputs and all $\ell$ monomial terms is shown empirically to experience a phase transition. Crucially, the same transition also presents itself in our ability to reject all irrelevant features and monomials as well. In the regime where our method is statistically powerful, its computational complexity is interestingly on par with Lasso based heuristics. The presented work fills a void in terms of a lack of powerful disciplined nonlinear sparse regression methods in high-dimensional settings. Our method is shown empirically to scale to regression problems with $n\approx 10,000$ observations for input dimension $p\approx 1,000$.

Sparse High-Dimensional Regression: Exact Scalable Algorithms and Phase Transitions

We present a novel binary convex reformulation of the sparse regression problem that constitutes a new duality perspective. We devise a new cutting plane method and provide evidence that it can solve to provable optimality the sparse regression problem for sample sizes n and number of regressors p in the 100,000s, that is two orders of magnitude better than the current state of the art, in seconds. The ability to solve the problem for very high dimensions allows us to observe new phase transition phenomena. Contrary to traditional complexity theory which suggests that the difficulty of a problem increases with problem size, the sparse regression problem has the property that as the number of samples $n$ increases the problem becomes easier in that the solution recovers 100% of the true signal, and our approach solves the problem extremely fast (in fact faster than Lasso), while for small number of samples n, our approach takes a larger amount of time to solve the problem, but importantly the optimal solution provides a statistically more relevant regressor. We argue that our exact sparse regression approach presents a superior alternative over heuristic methods available at present.