From Distributional Robustness to Robust Statistics: A Confidence Sets Perspective

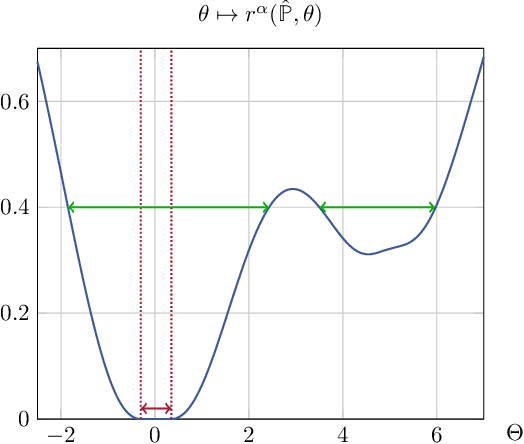
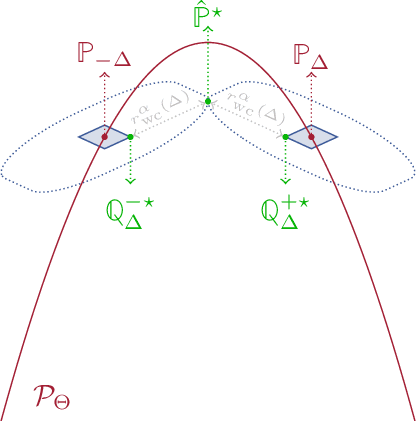
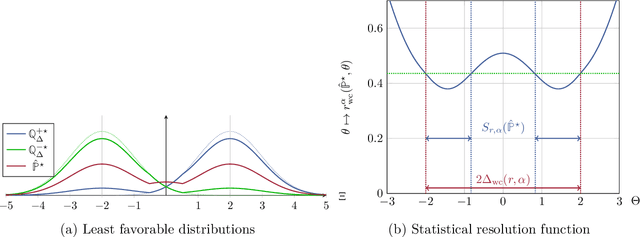
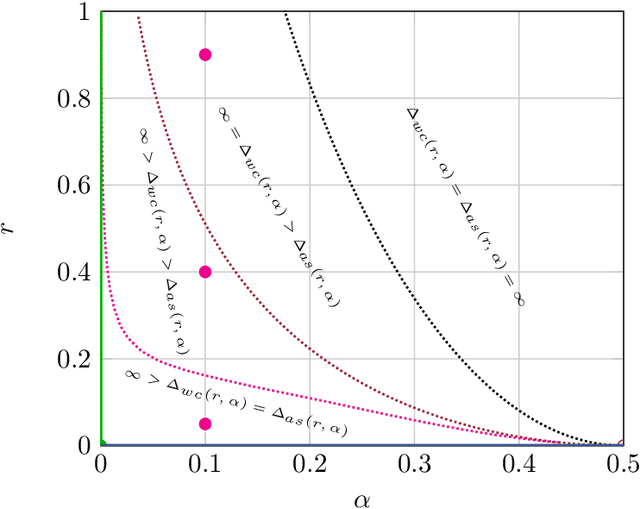
We establish a connection between distributionally robust optimization (DRO) and classical robust statistics. We demonstrate that this connection arises naturally in the context of estimation under data corruption, where the goal is to construct ``minimal'' confidence sets for the unknown data-generating distribution. Specifically, we show that a DRO ambiguity set, based on the Kullback-Leibler divergence and total variation distance, is uniformly minimal, meaning it represents the smallest confidence set that contains the unknown distribution with at a given confidence power. Moreover, we prove that when parametric assumptions are imposed on the unknown distribution, the ambiguity set is never larger than a confidence set based on the optimal estimator proposed by Huber. This insight reveals that the commonly observed conservatism of DRO formulations is not intrinsic to these formulations themselves but rather stems from the non-parametric framework in which these formulations are employed.

See Beyond Seeing: Robust 3D Object Detection from Point Clouds via Cross-Modal Hallucination

This paper presents a novel framework for robust 3D object detection from point clouds via cross-modal hallucination. Our proposed approach is agnostic to either hallucination direction between LiDAR and 4D radar. We introduce multiple alignments on both spatial and feature levels to achieve simultaneous backbone refinement and hallucination generation. Specifically, spatial alignment is proposed to deal with the geometry discrepancy for better instance matching between LiDAR and radar. The feature alignment step further bridges the intrinsic attribute gap between the sensing modalities and stabilizes the training. The trained object detection models can deal with difficult detection cases better, even though only single-modal data is used as the input during the inference stage. Extensive experiments on the View-of-Delft (VoD) dataset show that our proposed method outperforms the state-of-the-art (SOTA) methods for both radar and LiDAR object detection while maintaining competitive efficiency in runtime.