Real-Time Algorithms for Game-Theoretic Motion Planning and Control in Autonomous Racing using Near-Potential Function

Autonomous racing extends beyond the challenge of controlling a racecar at its physical limits. Professional racers employ strategic maneuvers to outwit other competing opponents to secure victory. While modern control algorithms can achieve human-level performance by computing offline racing lines for single-car scenarios, research on real-time algorithms for multi-car autonomous racing is limited. To bridge this gap, we develop game-theoretic modeling framework that incorporates the competitive aspect of autonomous racing like overtaking and blocking through a novel policy parametrization, while operating the car at its limit. Furthermore, we propose an algorithmic approach to compute the (approximate) Nash equilibrium strategy, which represents the optimal approach in the presence of competing agents. Specifically, we introduce an algorithm inspired by recently introduced framework of dynamic near-potential function, enabling real-time computation of the Nash equilibrium. Our approach comprises two phases: offline and online. During the offline phase, we use simulated racing data to learn a near-potential function that approximates utility changes for agents. This function facilitates the online computation of approximate Nash equilibria by maximizing its value. We evaluate our method in a head-to-head 3-car racing scenario, demonstrating superior performance compared to several existing baselines.

Decentralized Learning in General-sum Markov Games

The Markov game framework is widely used to model interactions among agents with heterogeneous utilities in dynamic and uncertain societal-scale systems. In these systems, agents typically operate in a decentralized manner due to privacy and scalability concerns, often acting without any information about other agents. The design and analysis of decentralized learning algorithms that provably converge to rational outcomes remain elusive, especially beyond Markov zero-sum games and Markov potential games, which do not adequately capture the nature of many real-world interactions that is neither fully competitive nor fully cooperative. This paper investigates the design of decentralized learning algorithms for general-sum Markov games, aiming to provide provable guarantees of convergence to approximate Nash equilibria in the long run. Our approach builds on constructing a Markov Near-Potential Function (MNPF) to address the intractability of designing algorithms that converge to exact Nash equilibria. We demonstrate that MNPFs play a central role in ensuring the convergence of an actor-critic-based decentralized learning algorithm to approximate Nash equilibria. By leveraging a two-timescale approach, where Q-function estimates are updated faster than policy updates, we show that the system converges to a level set of the MNPF over the set of approximate Nash equilibria. This convergence result is further strengthened if the set of Nash equilibria is assumed to be finite. Our findings provide a new perspective on the analysis and design of decentralized learning algorithms in multi-agent systems.

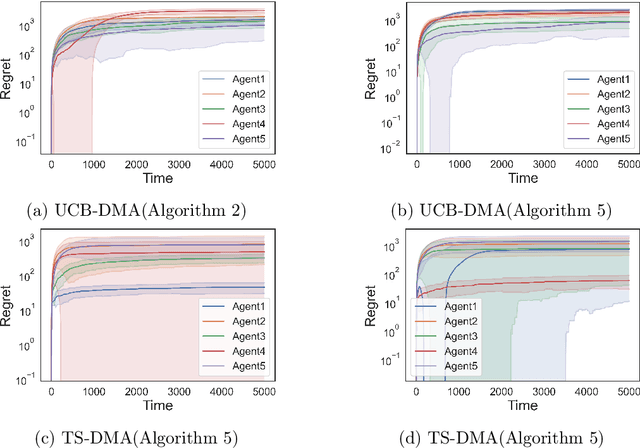
Markov $α$-Potential Games: Equilibrium Approximation and Regret Analysis

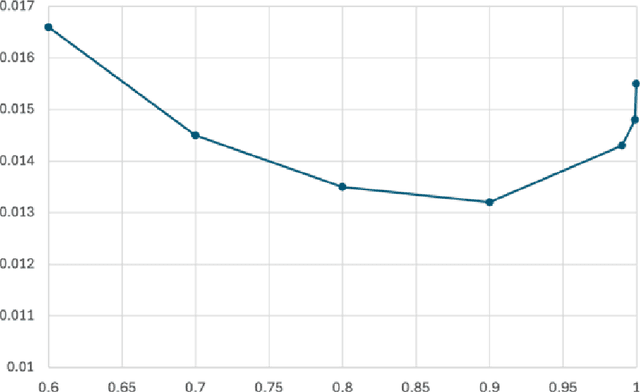
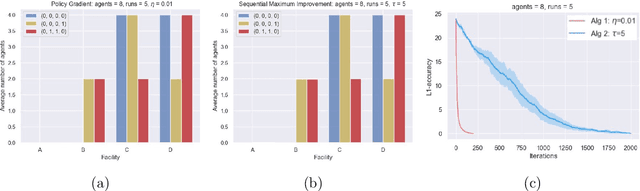
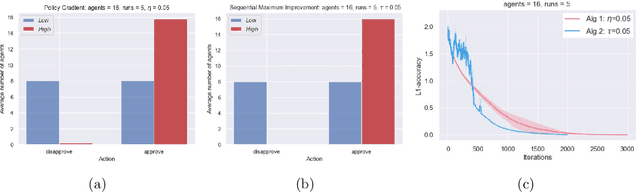
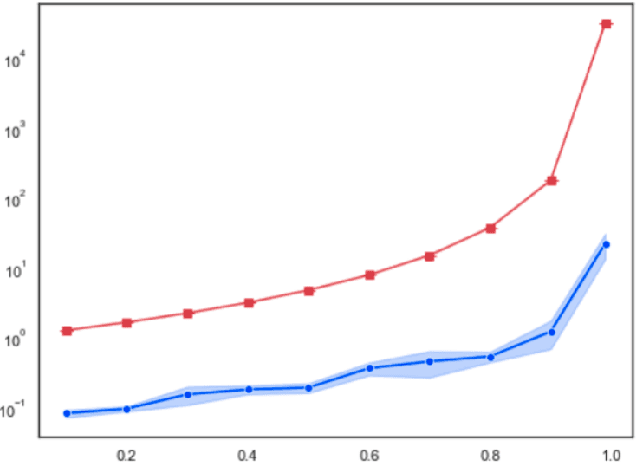
This paper proposes a new framework to study multi-agent interaction in Markov games: Markov $\alpha$-potential games. Markov potential games are special cases of Markov $\alpha$-potential games, so are two important and practically significant classes of games: Markov congestion games and perturbed Markov team games. In this paper, {$\alpha$-potential} functions for both games are provided and the gap $\alpha$ is characterized with respect to game parameters. Two algorithms -- the projected gradient-ascent algorithm and the sequential maximum improvement smoothed best response dynamics -- are introduced for approximating the stationary Nash equilibrium in Markov $\alpha$-potential games. The Nash-regret for each algorithm is shown to scale sub-linearly in time horizon. Our analysis and numerical experiments demonstrates that simple algorithms are capable of finding approximate equilibrium in Markov $\alpha$-potential games.

Convergent First-Order Methods for Bi-level Optimization and Stackelberg Games

We propose an algorithm to solve a class of bi-level optimization problems using only first-order information. In particular, we focus on a class where the inner minimization has unique solutions. Unlike contemporary algorithms, our algorithm does not require the use of an oracle estimator for the gradient of the bi-level objective or an approximate solver for the inner problem. Instead, we alternate between descending on the inner problem using na\"ive optimization methods and descending on the upper-level objective function using specially constructed gradient estimators. We provide non-asymptotic convergence rates to stationary points of the bi-level objective in the absence of convexity of the closed-loop function and further show asymptotic convergence to only local minima of the bi-level problem. The approach is inspired by ideas from the literature on two-timescale stochastic approximation algorithms.

Decentralized, Communication- and Coordination-free Learning in Structured Matching Markets

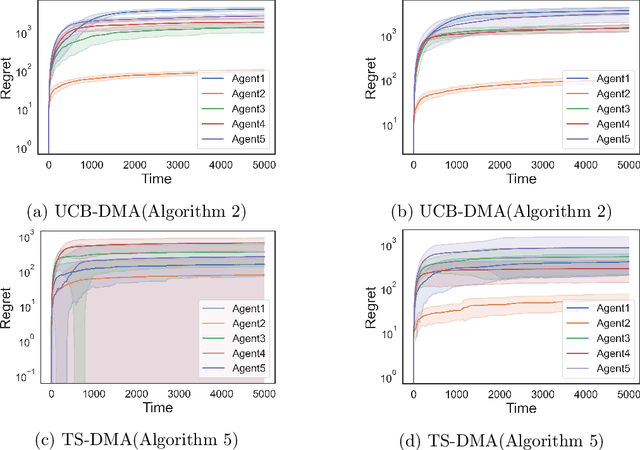
We study the problem of online learning in competitive settings in the context of two-sided matching markets. In particular, one side of the market, the agents, must learn about their preferences over the other side, the firms, through repeated interaction while competing with other agents for successful matches. We propose a class of decentralized, communication- and coordination-free algorithms that agents can use to reach to their stable match in structured matching markets. In contrast to prior works, the proposed algorithms make decisions based solely on an agent's own history of play and requires no foreknowledge of the firms' preferences. Our algorithms are constructed by splitting up the statistical problem of learning one's preferences, from noisy observations, from the problem of competing for firms. We show that under realistic structural assumptions on the underlying preferences of the agents and firms, the proposed algorithms incur a regret which grows at most logarithmically in the time horizon. Our results show that, in the case of matching markets, competition need not drastically affect the performance of decentralized, communication and coordination free online learning algorithms.

Independent and Decentralized Learning in Markov Potential Games

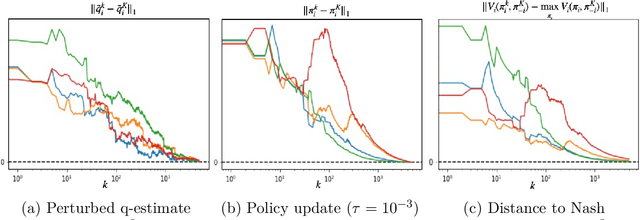
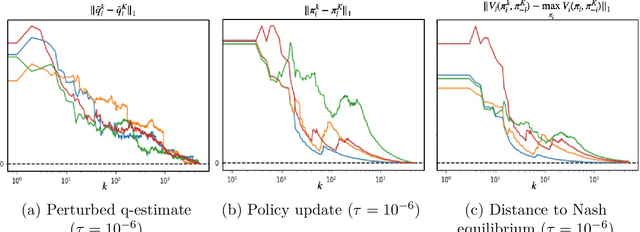
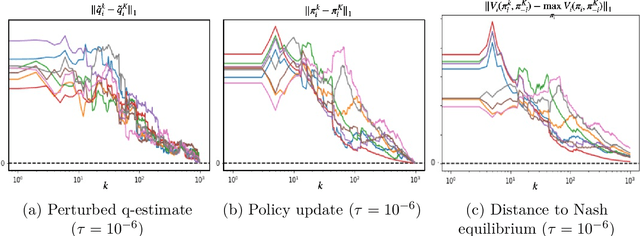
We propose a multi-agent reinforcement learning dynamics, and analyze its convergence properties in infinite-horizon discounted Markov potential games. We focus on the independent and decentralized setting, where players can only observe the realized state and their own reward in every stage. Players do not have knowledge of the game model, and cannot coordinate with each other. In each stage of our learning dynamics, players update their estimate of a perturbed Q-function that evaluates their total contingent payoff based on the realized one-stage reward in an asynchronous manner. Then, players independently update their policies by incorporating a smoothed optimal one-stage deviation strategy based on the estimated Q-function. A key feature of the learning dynamics is that the Q-function estimates are updated at a faster timescale than the policies. We prove that the policies induced by our learning dynamics converge to a stationary Nash equilibrium in Markov potential games with probability 1. Our results build on the theory of two timescale asynchronous stochastic approximation, and new analysis on the monotonicity of potential function along the trajectory of policy updates in Markov potential games.

Zeroth-Order Methods for Convex-Concave Minmax Problems: Applications to Decision-Dependent Risk Minimization

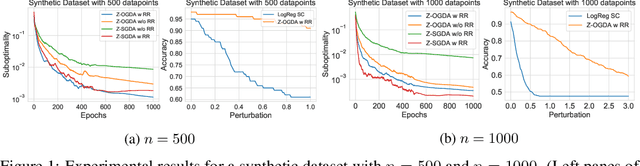
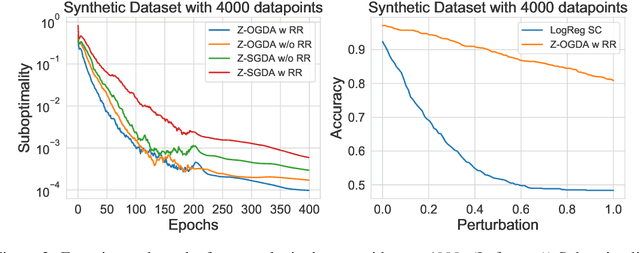
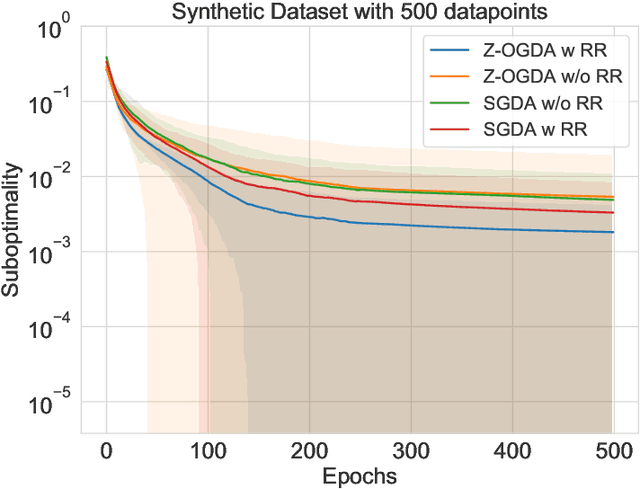
Min-max optimization is emerging as a key framework for analyzing problems of robustness to strategically and adversarially generated data. We propose a random reshuffling-based gradient free Optimistic Gradient Descent-Ascent algorithm for solving convex-concave min-max problems with finite sum structure. We prove that the algorithm enjoys the same convergence rate as that of zeroth-order algorithms for convex minimization problems. We further specialize the algorithm to solve distributionally robust, decision-dependent learning problems, where gradient information is not readily available. Through illustrative simulations, we observe that our proposed approach learns models that are simultaneously robust against adversarial distribution shifts and strategic decisions from the data sources, and outperforms existing methods from the strategic classification literature.