Real-Time Algorithms for Game-Theoretic Motion Planning and Control in Autonomous Racing using Near-Potential Function

Autonomous racing extends beyond the challenge of controlling a racecar at its physical limits. Professional racers employ strategic maneuvers to outwit other competing opponents to secure victory. While modern control algorithms can achieve human-level performance by computing offline racing lines for single-car scenarios, research on real-time algorithms for multi-car autonomous racing is limited. To bridge this gap, we develop game-theoretic modeling framework that incorporates the competitive aspect of autonomous racing like overtaking and blocking through a novel policy parametrization, while operating the car at its limit. Furthermore, we propose an algorithmic approach to compute the (approximate) Nash equilibrium strategy, which represents the optimal approach in the presence of competing agents. Specifically, we introduce an algorithm inspired by recently introduced framework of dynamic near-potential function, enabling real-time computation of the Nash equilibrium. Our approach comprises two phases: offline and online. During the offline phase, we use simulated racing data to learn a near-potential function that approximates utility changes for agents. This function facilitates the online computation of approximate Nash equilibria by maximizing its value. We evaluate our method in a head-to-head 3-car racing scenario, demonstrating superior performance compared to several existing baselines.

Decentralized Learning in General-sum Markov Games

The Markov game framework is widely used to model interactions among agents with heterogeneous utilities in dynamic and uncertain societal-scale systems. In these systems, agents typically operate in a decentralized manner due to privacy and scalability concerns, often acting without any information about other agents. The design and analysis of decentralized learning algorithms that provably converge to rational outcomes remain elusive, especially beyond Markov zero-sum games and Markov potential games, which do not adequately capture the nature of many real-world interactions that is neither fully competitive nor fully cooperative. This paper investigates the design of decentralized learning algorithms for general-sum Markov games, aiming to provide provable guarantees of convergence to approximate Nash equilibria in the long run. Our approach builds on constructing a Markov Near-Potential Function (MNPF) to address the intractability of designing algorithms that converge to exact Nash equilibria. We demonstrate that MNPFs play a central role in ensuring the convergence of an actor-critic-based decentralized learning algorithm to approximate Nash equilibria. By leveraging a two-timescale approach, where Q-function estimates are updated faster than policy updates, we show that the system converges to a level set of the MNPF over the set of approximate Nash equilibria. This convergence result is further strengthened if the set of Nash equilibria is assumed to be finite. Our findings provide a new perspective on the analysis and design of decentralized learning algorithms in multi-agent systems.

Hacking Predictors Means Hacking Cars: Using Sensitivity Analysis to Identify Trajectory Prediction Vulnerabilities for Autonomous Driving Security

Adversarial attacks on learning-based trajectory predictors have already been demonstrated. However, there are still open questions about the effects of perturbations on trajectory predictor inputs other than state histories, and how these attacks impact downstream planning and control. In this paper, we conduct a sensitivity analysis on two trajectory prediction models, Trajectron++ and AgentFormer. We observe that between all inputs, almost all of the perturbation sensitivities for Trajectron++ lie only within the most recent state history time point, while perturbation sensitivities for AgentFormer are spread across state histories over time. We additionally demonstrate that, despite dominant sensitivity on state history perturbations, an undetectable image map perturbation made with the Fast Gradient Sign Method can induce large prediction error increases in both models. Even though image maps may contribute slightly to the prediction output of both models, this result reveals that rather than being robust to adversarial image perturbations, trajectory predictors are susceptible to image attacks. Using an optimization-based planner and example perturbations crafted from sensitivity results, we show how this vulnerability can cause a vehicle to come to a sudden stop from moderate driving speeds.

Markov $α$-Potential Games: Equilibrium Approximation and Regret Analysis

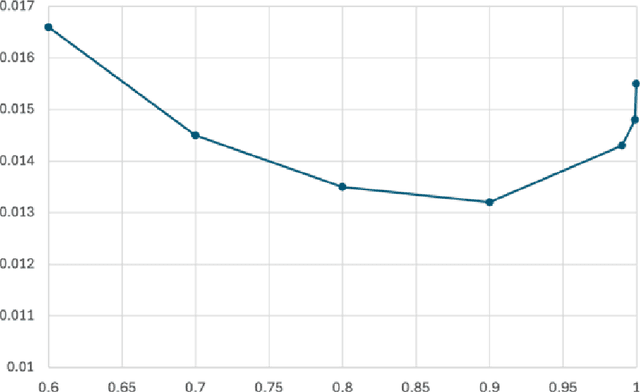
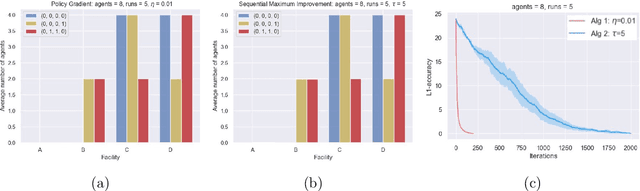
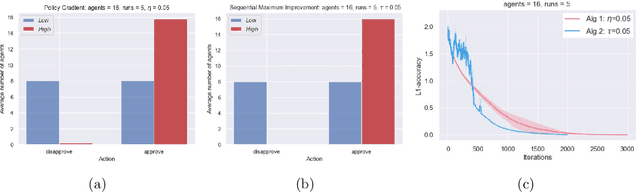
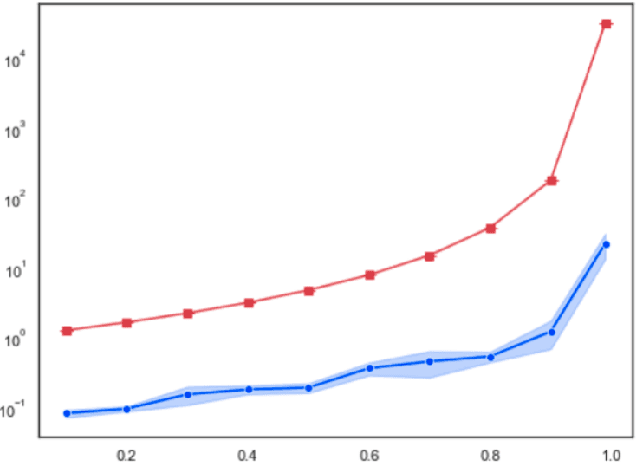
This paper proposes a new framework to study multi-agent interaction in Markov games: Markov $\alpha$-potential games. Markov potential games are special cases of Markov $\alpha$-potential games, so are two important and practically significant classes of games: Markov congestion games and perturbed Markov team games. In this paper, {$\alpha$-potential} functions for both games are provided and the gap $\alpha$ is characterized with respect to game parameters. Two algorithms -- the projected gradient-ascent algorithm and the sequential maximum improvement smoothed best response dynamics -- are introduced for approximating the stationary Nash equilibrium in Markov $\alpha$-potential games. The Nash-regret for each algorithm is shown to scale sub-linearly in time horizon. Our analysis and numerical experiments demonstrates that simple algorithms are capable of finding approximate equilibrium in Markov $\alpha$-potential games.

Representation Learning via Manifold Flattening and Reconstruction

This work proposes an algorithm for explicitly constructing a pair of neural networks that linearize and reconstruct an embedded submanifold, from finite samples of this manifold. Our such-generated neural networks, called Flattening Networks (FlatNet), are theoretically interpretable, computationally feasible at scale, and generalize well to test data, a balance not typically found in manifold-based learning methods. We present empirical results and comparisons to other models on synthetic high-dimensional manifold data and 2D image data. Our code is publicly available.

Towards Dynamic Causal Discovery with Rare Events: A Nonparametric Conditional Independence Test

Causal phenomena associated with rare events occur across a wide range of engineering problems, such as risk-sensitive safety analysis, accident analysis and prevention, and extreme value theory. However, current methods for causal discovery are often unable to uncover causal links, between random variables in a dynamic setting, that manifest only when the variables first experience low-probability realizations. To address this issue, we introduce a novel statistical independence test on data collected from time-invariant dynamical systems in which rare but consequential events occur. In particular, we exploit the time-invariance of the underlying data to construct a superimposed dataset of the system state before rare events happen at different timesteps. We then design a conditional independence test on the reorganized data. We provide non-asymptotic sample complexity bounds for the consistency of our method, and validate its performance across various simulated and real-world datasets, including incident data collected from the Caltrans Performance Measurement System (PeMS). Code containing the datasets and experiments is publicly available.

Lyapunov Design for Robust and Efficient Robotic Reinforcement Learning

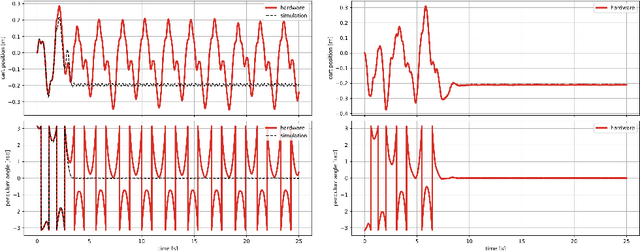
Recent advances in the reinforcement learning (RL) literature have enabled roboticists to automatically train complex policies in simulated environments. However, due to the poor sample complexity of these methods, solving reinforcement learning problems using real-world data remains a challenging problem. This paper introduces a novel cost-shaping method which aims to reduce the number of samples needed to learn a stabilizing controller. The method adds a term involving a control Lyapunov function (CLF) -- an `energy-like' function from the model-based control literature -- to typical cost formulations. Theoretical results demonstrate the new costs lead to stabilizing controllers when smaller discount factors are used, which is well-known to reduce sample complexity. Moreover, the addition of the CLF term `robustifies' the search for a stabilizing controller by ensuring that even highly sub-optimal polices will stabilize the system. We demonstrate our approach with two hardware examples where we learn stabilizing controllers for a cartpole and an A1 quadruped with only seconds and a few minutes of fine-tuning data, respectively.

Decentralized, Communication- and Coordination-free Learning in Structured Matching Markets

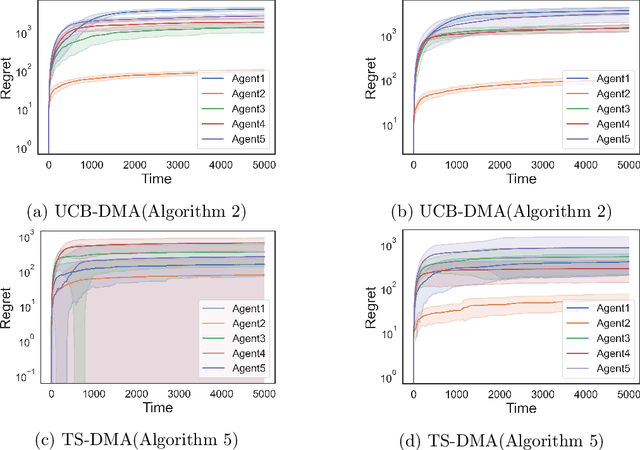
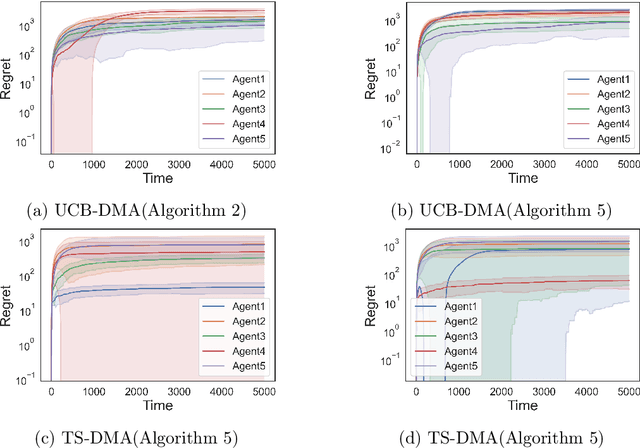
We study the problem of online learning in competitive settings in the context of two-sided matching markets. In particular, one side of the market, the agents, must learn about their preferences over the other side, the firms, through repeated interaction while competing with other agents for successful matches. We propose a class of decentralized, communication- and coordination-free algorithms that agents can use to reach to their stable match in structured matching markets. In contrast to prior works, the proposed algorithms make decisions based solely on an agent's own history of play and requires no foreknowledge of the firms' preferences. Our algorithms are constructed by splitting up the statistical problem of learning one's preferences, from noisy observations, from the problem of competing for firms. We show that under realistic structural assumptions on the underlying preferences of the agents and firms, the proposed algorithms incur a regret which grows at most logarithmically in the time horizon. Our results show that, in the case of matching markets, competition need not drastically affect the performance of decentralized, communication and coordination free online learning algorithms.

Independent and Decentralized Learning in Markov Potential Games

We propose a multi-agent reinforcement learning dynamics, and analyze its convergence properties in infinite-horizon discounted Markov potential games. We focus on the independent and decentralized setting, where players can only observe the realized state and their own reward in every stage. Players do not have knowledge of the game model, and cannot coordinate with each other. In each stage of our learning dynamics, players update their estimate of a perturbed Q-function that evaluates their total contingent payoff based on the realized one-stage reward in an asynchronous manner. Then, players independently update their policies by incorporating a smoothed optimal one-stage deviation strategy based on the estimated Q-function. A key feature of the learning dynamics is that the Q-function estimates are updated at a faster timescale than the policies. We prove that the policies induced by our learning dynamics converge to a stationary Nash equilibrium in Markov potential games with probability 1. Our results build on the theory of two timescale asynchronous stochastic approximation, and new analysis on the monotonicity of potential function along the trajectory of policy updates in Markov potential games.

Residual Networks: Lyapunov Stability and Convex Decomposition

While training error of most deep neural networks degrades as the depth of the network increases, residual networks appear to be an exception. We show that the main reason for this is the Lyapunov stability of the gradient descent algorithm: for an arbitrarily chosen step size, the equilibria of the gradient descent are most likely to remain stable for the parametrization of residual networks. We then present an architecture with a pair of residual networks to approximate a large class of functions by decomposing them into a convex and a concave part. Some parameters of this model are shown to change little during training, and this imperfect optimization prevents overfitting the data and leads to solutions with small Lipschitz constants, while providing clues about the generalization of other deep networks.