Fernando Castaneda
Lyapunov Design for Robust and Efficient Robotic Reinforcement Learning
Aug 13, 2022
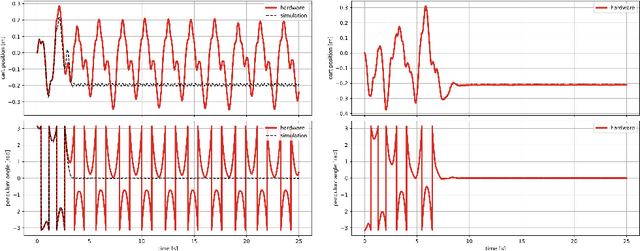


Abstract:Recent advances in the reinforcement learning (RL) literature have enabled roboticists to automatically train complex policies in simulated environments. However, due to the poor sample complexity of these methods, solving reinforcement learning problems using real-world data remains a challenging problem. This paper introduces a novel cost-shaping method which aims to reduce the number of samples needed to learn a stabilizing controller. The method adds a term involving a control Lyapunov function (CLF) -- an `energy-like' function from the model-based control literature -- to typical cost formulations. Theoretical results demonstrate the new costs lead to stabilizing controllers when smaller discount factors are used, which is well-known to reduce sample complexity. Moreover, the addition of the CLF term `robustifies' the search for a stabilizing controller by ensuring that even highly sub-optimal polices will stabilize the system. We demonstrate our approach with two hardware examples where we learn stabilizing controllers for a cartpole and an A1 quadruped with only seconds and a few minutes of fine-tuning data, respectively.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge