Robustness Certificates for Implicit Neural Networks: A Mixed Monotone Contractive Approach
Paper and Code
Dec 10, 2021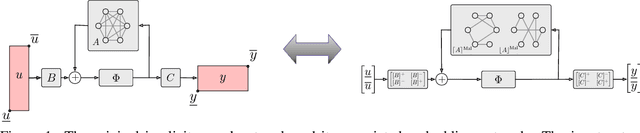
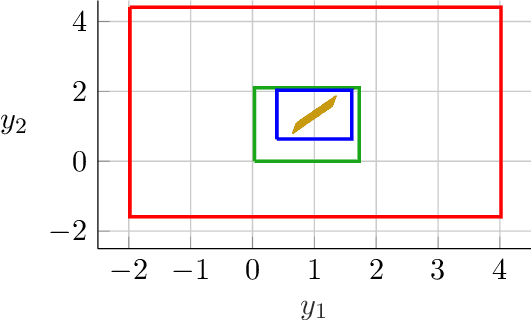
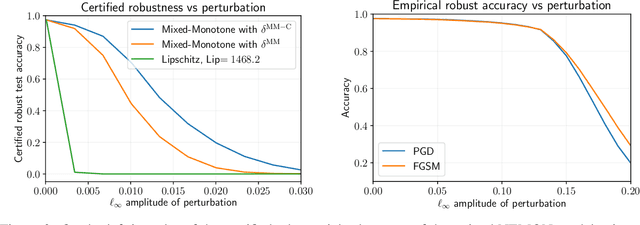
Implicit neural networks are a general class of learning models that replace the layers in traditional feedforward models with implicit algebraic equations. Compared to traditional learning models, implicit networks offer competitive performance and reduced memory consumption. However, they can remain brittle with respect to input adversarial perturbations. This paper proposes a theoretical and computational framework for robustness verification of implicit neural networks; our framework blends together mixed monotone systems theory and contraction theory. First, given an implicit neural network, we introduce a related embedded network and show that, given an $\ell_\infty$-norm box constraint on the input, the embedded network provides an $\ell_\infty$-norm box overapproximation for the output of the given network. Second, using $\ell_{\infty}$-matrix measures, we propose sufficient conditions for well-posedness of both the original and embedded system and design an iterative algorithm to compute the $\ell_{\infty}$-norm box robustness margins for reachability and classification problems. Third, of independent value, we propose a novel relative classifier variable that leads to tighter bounds on the certified adversarial robustness in classification problems. Finally, we perform numerical simulations on a Non-Euclidean Monotone Operator Network (NEMON) trained on the MNIST dataset. In these simulations, we compare the accuracy and run time of our mixed monotone contractive approach with the existing robustness verification approaches in the literature for estimating the certified adversarial robustness.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge