Robust Training and Verification of Implicit Neural Networks: A Non-Euclidean Contractive Approach

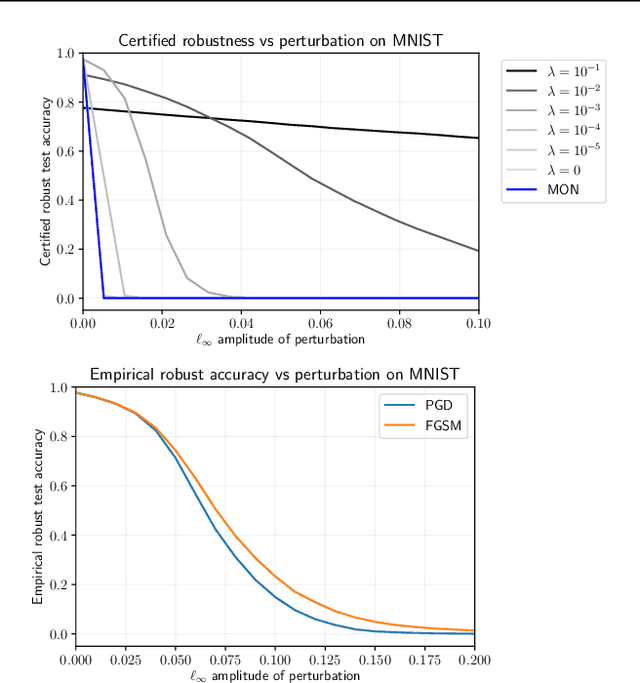
This paper proposes a theoretical and computational framework for training and robustness verification of implicit neural networks based upon non-Euclidean contraction theory. The basic idea is to cast the robustness analysis of a neural network as a reachability problem and use (i) the $\ell_{\infty}$-norm input-output Lipschitz constant and (ii) the tight inclusion function of the network to over-approximate its reachable sets. First, for a given implicit neural network, we use $\ell_{\infty}$-matrix measures to propose sufficient conditions for its well-posedness, design an iterative algorithm to compute its fixed points, and provide upper bounds for its $\ell_\infty$-norm input-output Lipschitz constant. Second, we introduce a related embedded network and show that the embedded network can be used to provide an $\ell_\infty$-norm box over-approximation of the reachable sets of the original network. Moreover, we use the embedded network to design an iterative algorithm for computing the upper bounds of the original system's tight inclusion function. Third, we use the upper bounds of the Lipschitz constants and the upper bounds of the tight inclusion functions to design two algorithms for the training and robustness verification of implicit neural networks. Finally, we apply our algorithms to train implicit neural networks on the MNIST dataset and compare the robustness of our models with the models trained via existing approaches in the literature.

Comparative Analysis of Interval Reachability for Robust Implicit and Feedforward Neural Networks

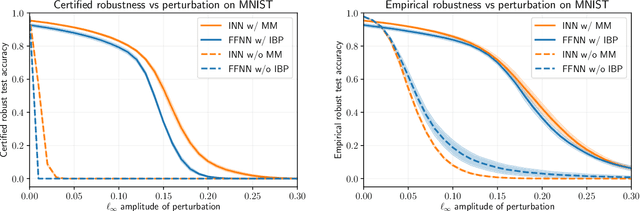
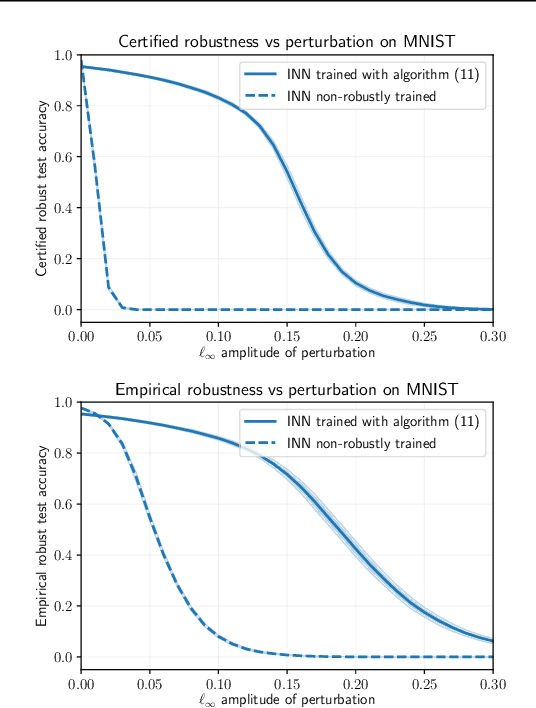
We use interval reachability analysis to obtain robustness guarantees for implicit neural networks (INNs). INNs are a class of implicit learning models that use implicit equations as layers and have been shown to exhibit several notable benefits over traditional deep neural networks. We first establish that tight inclusion functions of neural networks, which provide the tightest rectangular over-approximation of an input-output map, lead to sharper robustness guarantees than the well-studied robustness measures of local Lipschitz constants. Like Lipschitz constants, tight inclusions functions are computationally challenging to obtain, and we thus propose using mixed monotonicity and contraction theory to obtain computationally efficient estimates of tight inclusion functions for INNs. We show that our approach performs at least as well as, and generally better than, applying state-of-the-art interval bound propagation methods to INNs. We design a novel optimization problem for training robust INNs and we provide empirical evidence that suitably-trained INNs can be more robust than comparably-trained feedforward networks.

Robustness Certificates for Implicit Neural Networks: A Mixed Monotone Contractive Approach

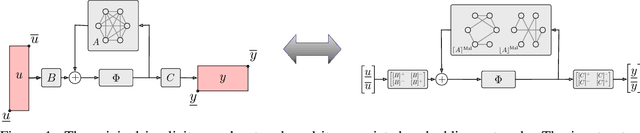
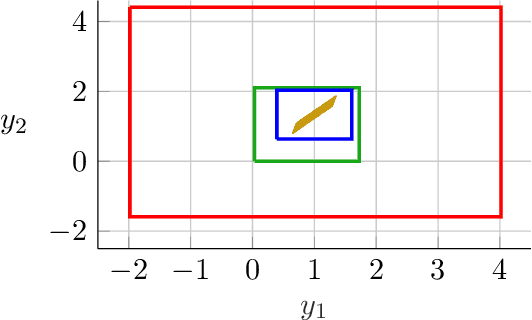
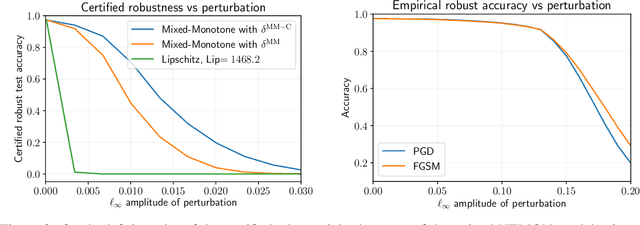
Implicit neural networks are a general class of learning models that replace the layers in traditional feedforward models with implicit algebraic equations. Compared to traditional learning models, implicit networks offer competitive performance and reduced memory consumption. However, they can remain brittle with respect to input adversarial perturbations. This paper proposes a theoretical and computational framework for robustness verification of implicit neural networks; our framework blends together mixed monotone systems theory and contraction theory. First, given an implicit neural network, we introduce a related embedded network and show that, given an $\ell_\infty$-norm box constraint on the input, the embedded network provides an $\ell_\infty$-norm box overapproximation for the output of the given network. Second, using $\ell_{\infty}$-matrix measures, we propose sufficient conditions for well-posedness of both the original and embedded system and design an iterative algorithm to compute the $\ell_{\infty}$-norm box robustness margins for reachability and classification problems. Third, of independent value, we propose a novel relative classifier variable that leads to tighter bounds on the certified adversarial robustness in classification problems. Finally, we perform numerical simulations on a Non-Euclidean Monotone Operator Network (NEMON) trained on the MNIST dataset. In these simulations, we compare the accuracy and run time of our mixed monotone contractive approach with the existing robustness verification approaches in the literature for estimating the certified adversarial robustness.

Extent-Compatible Control Barrier Functions

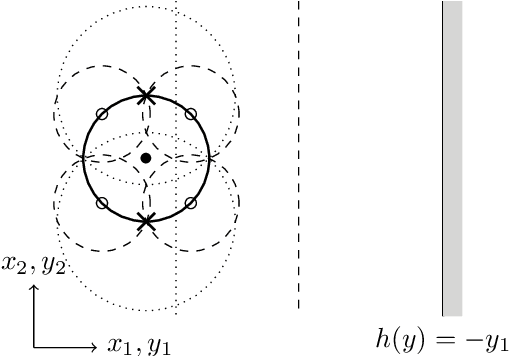
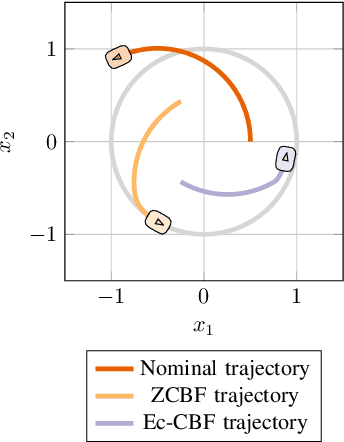
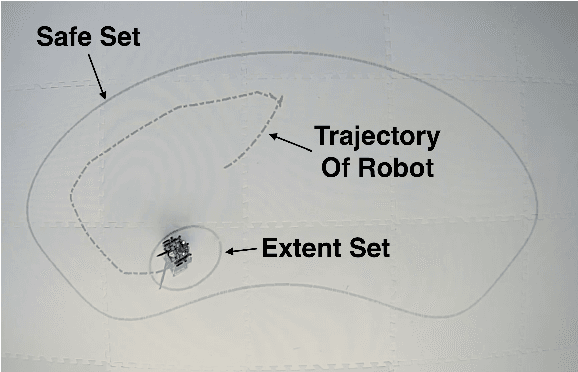
Safety requirements in dynamical systems are commonly enforced with set invariance constraints over a safe region of the state space. Control barrier functions, which are Lyapunov-like functions for guaranteeing set invariance, are an effective tool to enforce such constraints and guarantee safety when the system is represented as a point in the state space. In this paper, we introduce extent-compatible control barrier functions as a tool to enforce safety for the system including its volume (extent) in the physical world. In order to implement the extent-compatible control barrier functions framework, a sum-of-squares based optimization program is proposed. Since sum-of-squares programs can be computationally prohibitive, we additionally introduce a sampling based method in order to retain the computational advantage of a traditional barrier function based quadratic program controller. We prove that the proposed sampling based controller retains the guarantee for safety. Simulation and robotic implementation results are also provided.