Comparative Analysis of Interval Reachability for Robust Implicit and Feedforward Neural Networks
Paper and Code
Apr 01, 2022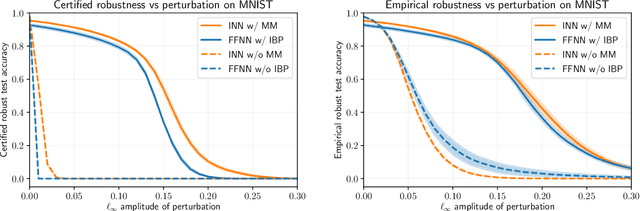
We use interval reachability analysis to obtain robustness guarantees for implicit neural networks (INNs). INNs are a class of implicit learning models that use implicit equations as layers and have been shown to exhibit several notable benefits over traditional deep neural networks. We first establish that tight inclusion functions of neural networks, which provide the tightest rectangular over-approximation of an input-output map, lead to sharper robustness guarantees than the well-studied robustness measures of local Lipschitz constants. Like Lipschitz constants, tight inclusions functions are computationally challenging to obtain, and we thus propose using mixed monotonicity and contraction theory to obtain computationally efficient estimates of tight inclusion functions for INNs. We show that our approach performs at least as well as, and generally better than, applying state-of-the-art interval bound propagation methods to INNs. We design a novel optimization problem for training robust INNs and we provide empirical evidence that suitably-trained INNs can be more robust than comparably-trained feedforward networks.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge