Similarity Matching Networks: Hebbian Learning and Convergence Over Multiple Time Scales

A recent breakthrough in biologically-plausible normative frameworks for dimensionality reduction is based upon the similarity matching cost function and the low-rank matrix approximation problem. Despite clear biological interpretation, successful application in several domains, and experimental validation, a formal complete convergence analysis remains elusive. Building on this framework, we consider and analyze a continuous-time neural network, the \emph{similarity matching network}, for principal subspace projection. Derived from a min-max-min objective, this biologically-plausible network consists of three coupled dynamics evolving at different time scales: neural dynamics, lateral synaptic dynamics, and feedforward synaptic dynamics at the fast, intermediate, and slow time scales, respectively. The feedforward and lateral synaptic dynamics consist of Hebbian and anti-Hebbian learning rules, respectively. By leveraging a multilevel optimization framework, we prove convergence of the dynamics in the offline setting. Specifically, at the first level (fast time scale), we show strong convexity of the cost function and global exponential convergence of the corresponding gradient-flow dynamics. At the second level (intermediate time scale), we prove strong concavity of the cost function and exponential convergence of the corresponding gradient-flow dynamics within the space of positive definite matrices. At the third and final level (slow time scale), we study a non-convex and non-smooth cost function, provide explicit expressions for its global minima, and prove almost sure convergence of the corresponding gradient-flow dynamics to the global minima. These results rely on two empirically motivated conjectures that are supported by thorough numerical experiments. Finally, we validate the effectiveness of our approach via a numerical example.

Contracting Dynamics for Time-Varying Convex Optimization

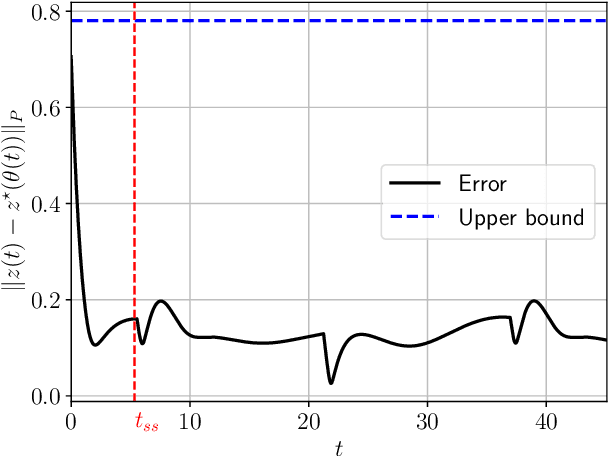
In this article, we provide a novel and broadly-applicable contraction-theoretic approach to continuous-time time-varying convex optimization. For any parameter-dependent contracting dynamics, we show that the tracking error between any solution trajectory and the equilibrium trajectory is uniformly upper bounded in terms of the contraction rate, the Lipschitz constant in which the parameter appears, and the rate of change of the parameter. To apply this result to time-varying convex optimization problems, we establish the strong infinitesimal contraction of dynamics solving three canonical problems, namely monotone inclusions, linear equality-constrained problems, and composite minimization problems. For each of these problems, we prove the sharpest-known rates of contraction and provide explicit tracking error bounds between solution trajectories and minimizing trajectories. We validate our theoretical results on two numerical examples.