Firing Rate Models as Associative Memory: Excitatory-Inhibitory Balance for Robust Retrieval

Firing rate models are dynamical systems widely used in applied and theoretical neuroscience to describe local cortical dynamics in neuronal populations. By providing a macroscopic perspective of neuronal activity, these models are essential for investigating oscillatory phenomena, chaotic behavior, and associative memory processes. Despite their widespread use, the application of firing rate models to associative memory networks has received limited mathematical exploration, and most existing studies are focused on specific models. Conversely, well-established associative memory designs, such as Hopfield networks, lack key biologically-relevant features intrinsic to firing rate models, including positivity and interpretable synaptic matrices that reflect excitatory and inhibitory interactions. To address this gap, we propose a general framework that ensures the emergence of re-scaled memory patterns as stable equilibria in the firing rate dynamics. Furthermore, we analyze the conditions under which the memories are locally and globally asymptotically stable, providing insights into constructing biologically-plausible and robust systems for associative memory retrieval.

Learning Minimum-Energy Controls from Heterogeneous Data

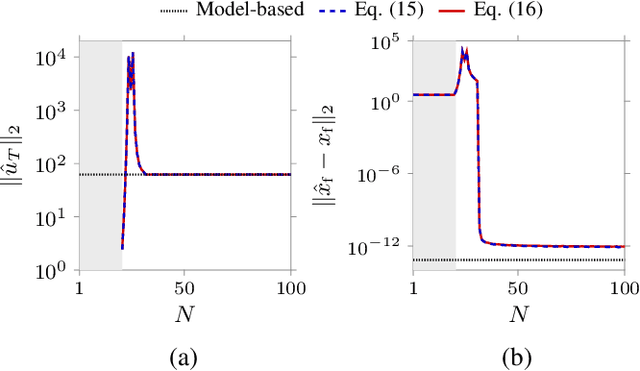
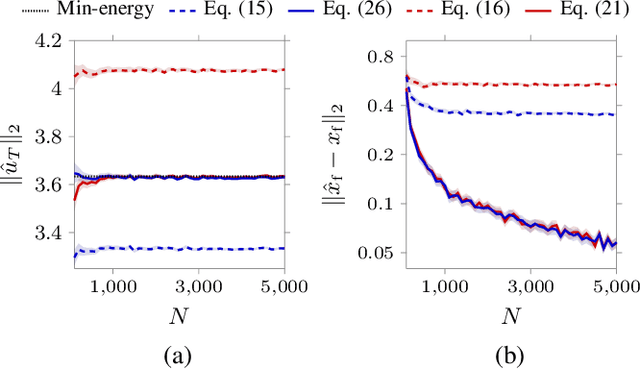
In this paper we study the problem of learning minimum-energy controls for linear systems from heterogeneous data. Specifically, we consider datasets comprising input, initial and final state measurements collected using experiments with different time horizons and arbitrary initial conditions. In this setting, we first establish a general representation of input and sampled state trajectories of the system based on the available data. Then, we leverage this data-based representation to derive closed-form data-driven expressions of minimum-energy controls for a wide range of control horizons. Further, we characterize the minimum number of data required to reconstruct the minimum-energy inputs, and discuss the numerical properties of our expressions. Finally, we investigate the effect of noise on our data-driven formulas, and, in the case of noise with known second-order statistics, we provide corrected expressions that converge asymptotically to the true optimal control inputs.