Learning Minimum-Energy Controls from Heterogeneous Data
Paper and Code
Jun 18, 2020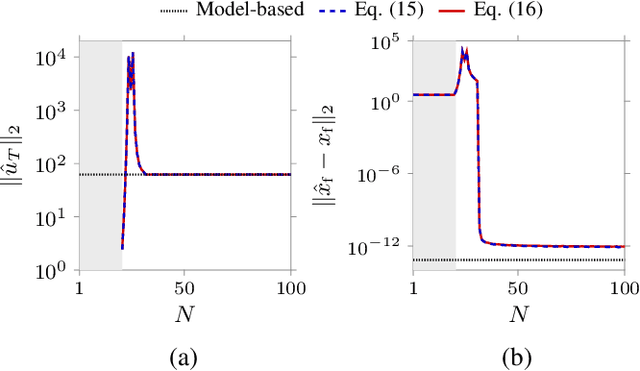
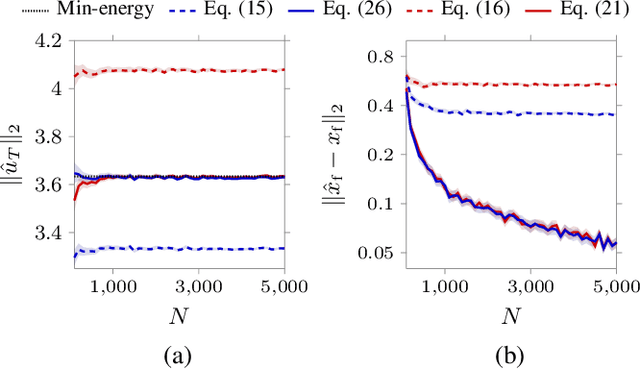
In this paper we study the problem of learning minimum-energy controls for linear systems from heterogeneous data. Specifically, we consider datasets comprising input, initial and final state measurements collected using experiments with different time horizons and arbitrary initial conditions. In this setting, we first establish a general representation of input and sampled state trajectories of the system based on the available data. Then, we leverage this data-based representation to derive closed-form data-driven expressions of minimum-energy controls for a wide range of control horizons. Further, we characterize the minimum number of data required to reconstruct the minimum-energy inputs, and discuss the numerical properties of our expressions. Finally, we investigate the effect of noise on our data-driven formulas, and, in the case of noise with known second-order statistics, we provide corrected expressions that converge asymptotically to the true optimal control inputs.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge