Online Subset Selection using $α$-Core with no Augmented Regret

We consider the problem of sequential sparse subset selections in an online learning setup. Assume that the set $[N]$ consists of $N$ distinct elements. On the $t^{\text{th}}$ round, a monotone reward function $f_t: 2^{[N]} \to \mathbb{R}_+,$ which assigns a non-negative reward to each subset of $[N],$ is revealed to a learner. The learner selects (perhaps randomly) a subset $S_t \subseteq [N]$ of $k$ elements before the reward function $f_t$ for that round is revealed $(k \leq N)$. As a consequence of its choice, the learner receives a reward of $f_t(S_t)$ on the $t^{\text{th}}$ round. The learner's goal is to design an online subset selection policy to maximize its expected cumulative reward accrued over a given time horizon. In this connection, we propose an online learning policy called SCore (Subset Selection with Core) that solves the problem for a large class of reward functions. The proposed SCore policy is based on a new concept of $\alpha$-Core, which is a generalization of the notion of Core from the cooperative game theory literature. We establish a learning guarantee for the SCore policy in terms of a new performance metric called $\alpha$-augmented regret. In this new metric, the power of the offline benchmark is suitably augmented compared to the online policy. We give several illustrative examples to show that a broad class of reward functions, including submodular, can be efficiently learned with the SCore policy. We also outline how the SCore policy can be used under a semi-bandit feedback model and conclude the paper with a number of open problems.

$k\texttt{-experts}$ -- Online Policies and Fundamental Limits

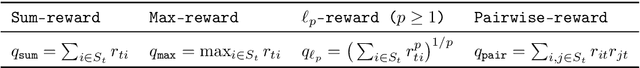
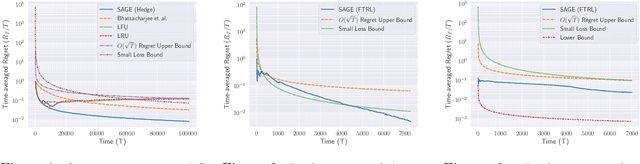
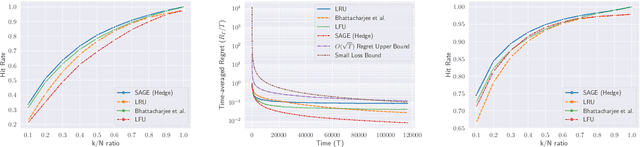
This paper introduces and studies the $k\texttt{-experts}$ problem -- a generalization of the classic Prediction with Expert's Advice (i.e., the $\texttt{Experts}$) problem. Unlike the $\texttt{Experts}$ problem, where the learner chooses exactly one expert, in this problem, the learner selects a subset of $k$ experts from a pool of $N$ experts at each round. The reward obtained by the learner at any round depends on the rewards of the selected experts. The $k\texttt{-experts}$ problem arises in many practical settings, including online ad placements, personalized news recommendations, and paging. Our primary goal is to design an online learning policy having a small regret. In this pursuit, we propose $\texttt{SAGE}$ ($\textbf{Sa}$mpled Hed$\textbf{ge}$) - a framework for designing efficient online learning policies by leveraging statistical sampling techniques. We show that, for many related problems, $\texttt{SAGE}$ improves upon the state-of-the-art bounds for regret and computational complexity. Furthermore, going beyond the notion of regret, we characterize the mistake bounds achievable by online learning policies for a class of stable loss functions. We conclude the paper by establishing a tight regret lower bound for a variant of the $k\texttt{-experts}$ problem and carrying out experiments with standard datasets.

Distributed Online Optimization with Byzantine Adversarial Agents

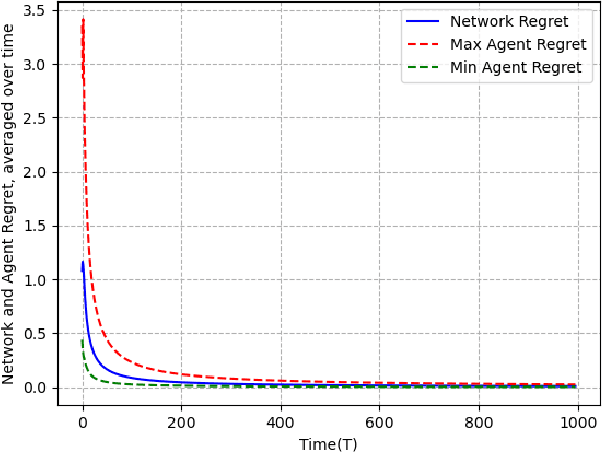
We study the problem of non-constrained, discrete-time, online distributed optimization in a multi-agent system where some of the agents do not follow the prescribed update rule either due to failures or malicious intentions. None of the agents have prior information about the identities of the faulty agents and any agent can communicate only with its immediate neighbours. At each time step, a Lipschitz strongly convex cost function is revealed locally to all the agents and the non-faulty agents update their states using their local information and the information obtained from their neighbours. We measure the performance of the online algorithm by comparing it to its offline version when the cost functions are known apriori. The difference between the same is termed as regret. Under sufficient conditions on the graph topology, the number and location of the adversaries, the defined regret grows sublinearly. We further conduct numerical experiments to validate our theoretical results.

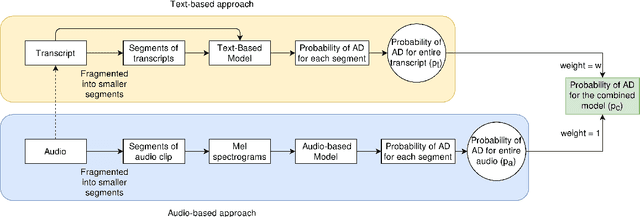
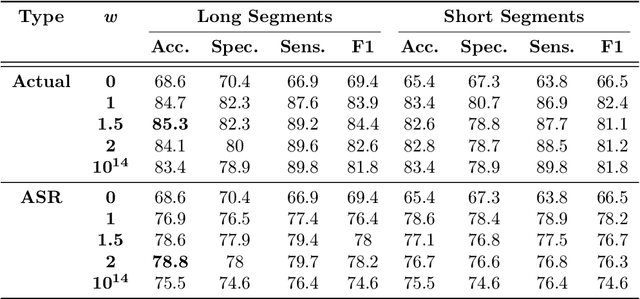
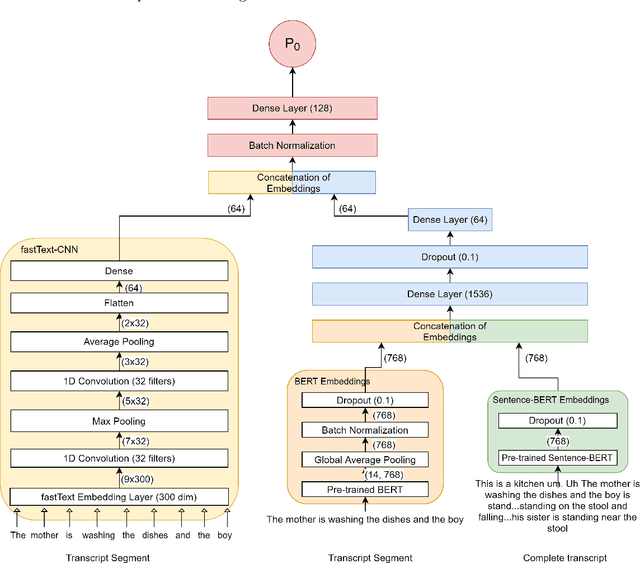
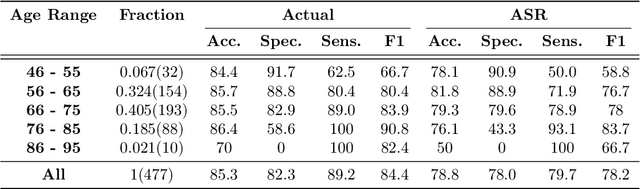
Multi-Modal Detection of Alzheimer's Disease from Speech and Text

Reliable detection of the prodromal stages of Alzheimer's disease (AD) remains difficult even today because, unlike other neurocognitive impairments, there is no definitive diagnosis of AD in vivo. In this context, existing research has shown that patients often develop language impairment even in mild AD conditions. We propose a multimodal deep learning method that utilizes speech and the corresponding transcript simultaneously to detect AD. For audio signals, the proposed audio-based network, a convolutional neural network (CNN) based model, predicts the diagnosis for multiple speech segments, which are combined for the final prediction. Similarly, we use contextual embedding extracted from BERT concatenated with a CNN-generated embedding for classifying the transcript. The individual predictions of the two models are then combined to make the final classification. We also perform experiments to analyze the model performance when Automated Speech Recognition (ASR) system generated transcripts are used instead of manual transcription in the text-based model. The proposed method achieves 85.3% 10-fold cross-validation accuracy when trained and evaluated on the Dementiabank Pitt corpus.