Samrat Mukhopadhyay
Online Learning for Approximately-Convex Functions with Long-term Adversarial Constraints
Aug 23, 2025Abstract:We study an online learning problem with long-term budget constraints in the adversarial setting. In this problem, at each round $t$, the learner selects an action from a convex decision set, after which the adversary reveals a cost function $f_t$ and a resource consumption function $g_t$. The cost and consumption functions are assumed to be $\alpha$-approximately convex - a broad class that generalizes convexity and encompasses many common non-convex optimization problems, including DR-submodular maximization, Online Vertex Cover, and Regularized Phase Retrieval. The goal is to design an online algorithm that minimizes cumulative cost over a horizon of length $T$ while approximately satisfying a long-term budget constraint of $B_T$. We propose an efficient first-order online algorithm that guarantees $O(\sqrt{T})$ $\alpha$-regret against the optimal fixed feasible benchmark while consuming at most $O(B_T \log T)+ \tilde{O}(\sqrt{T})$ resources in both full-information and bandit feedback settings. In the bandit feedback setting, our approach yields an efficient solution for the $\texttt{Adversarial Bandits with Knapsacks}$ problem with improved guarantees. We also prove matching lower bounds, demonstrating the tightness of our results. Finally, we characterize the class of $\alpha$-approximately convex functions and show that our results apply to a broad family of problems.
Follow The Approximate Sparse Leader for No-Regret Online Sparse Linear Approximation
Jan 07, 2025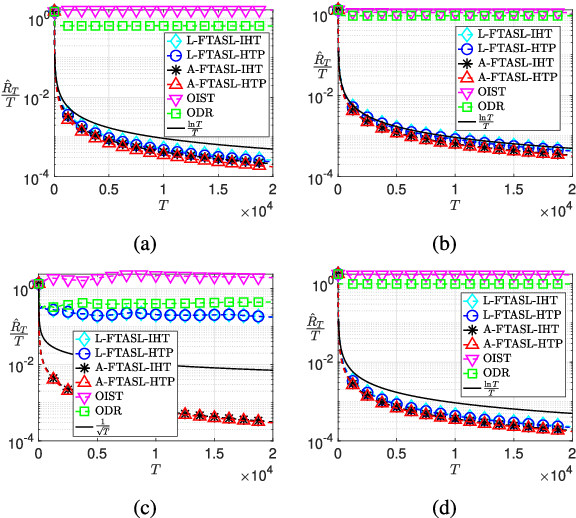
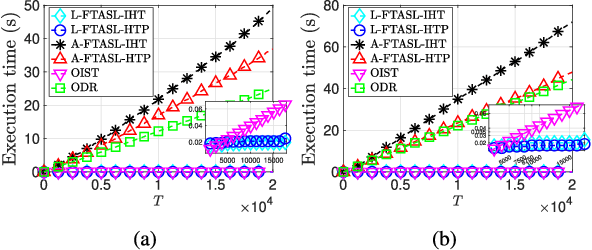

Abstract:We consider the problem of \textit{online sparse linear approximation}, where one predicts the best sparse approximation of a sequence of measurements in terms of linear combination of columns of a given measurement matrix. Such online prediction problems are ubiquitous, ranging from medical trials to web caching to resource allocation. The inherent difficulty of offline recovery also makes the online problem challenging. In this letter, we propose Follow-The-Approximate-Sparse-Leader, an efficient online meta-policy to address this online problem. Through a detailed theoretical analysis, we prove that under certain assumptions on the measurement sequence, the proposed policy enjoys a data-dependent sublinear upper bound on the static regret, which can range from logarithmic to square-root. Numerical simulations are performed to corroborate the theoretical findings and demonstrate the efficacy of the proposed online policy.
Online Subset Selection using $α$-Core with no Augmented Regret
Sep 29, 2022
Abstract:We consider the problem of sequential sparse subset selections in an online learning setup. Assume that the set $[N]$ consists of $N$ distinct elements. On the $t^{\text{th}}$ round, a monotone reward function $f_t: 2^{[N]} \to \mathbb{R}_+,$ which assigns a non-negative reward to each subset of $[N],$ is revealed to a learner. The learner selects (perhaps randomly) a subset $S_t \subseteq [N]$ of $k$ elements before the reward function $f_t$ for that round is revealed $(k \leq N)$. As a consequence of its choice, the learner receives a reward of $f_t(S_t)$ on the $t^{\text{th}}$ round. The learner's goal is to design an online subset selection policy to maximize its expected cumulative reward accrued over a given time horizon. In this connection, we propose an online learning policy called SCore (Subset Selection with Core) that solves the problem for a large class of reward functions. The proposed SCore policy is based on a new concept of $\alpha$-Core, which is a generalization of the notion of Core from the cooperative game theory literature. We establish a learning guarantee for the SCore policy in terms of a new performance metric called $\alpha$-augmented regret. In this new metric, the power of the offline benchmark is suitably augmented compared to the online policy. We give several illustrative examples to show that a broad class of reward functions, including submodular, can be efficiently learned with the SCore policy. We also outline how the SCore policy can be used under a semi-bandit feedback model and conclude the paper with a number of open problems.
$k\texttt{-experts}$ -- Online Policies and Fundamental Limits
Oct 15, 2021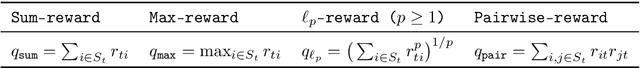
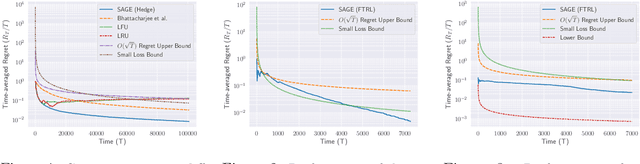

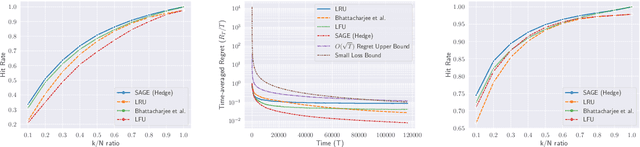
Abstract:This paper introduces and studies the $k\texttt{-experts}$ problem -- a generalization of the classic Prediction with Expert's Advice (i.e., the $\texttt{Experts}$) problem. Unlike the $\texttt{Experts}$ problem, where the learner chooses exactly one expert, in this problem, the learner selects a subset of $k$ experts from a pool of $N$ experts at each round. The reward obtained by the learner at any round depends on the rewards of the selected experts. The $k\texttt{-experts}$ problem arises in many practical settings, including online ad placements, personalized news recommendations, and paging. Our primary goal is to design an online learning policy having a small regret. In this pursuit, we propose $\texttt{SAGE}$ ($\textbf{Sa}$mpled Hed$\textbf{ge}$) - a framework for designing efficient online learning policies by leveraging statistical sampling techniques. We show that, for many related problems, $\texttt{SAGE}$ improves upon the state-of-the-art bounds for regret and computational complexity. Furthermore, going beyond the notion of regret, we characterize the mistake bounds achievable by online learning policies for a class of stable loss functions. We conclude the paper by establishing a tight regret lower bound for a variant of the $k\texttt{-experts}$ problem and carrying out experiments with standard datasets.
Dynamic Sample Complexity for Exact Sparse Recovery using Sequential Iterative Hard Thresholding
Feb 28, 2021
Abstract:In this paper we consider the problem of exact recovery of a fixed sparse vector with the measurement matrices sequentially arriving along with corresponding measurements. We propose an extension of the iterative hard thresholding (IHT) algorithm, termed as sequential IHT (SIHT) which breaks the total time horizon into several phases such that IHT is executed in each of these phases using a fixed measurement matrix obtained at the beginning of that phase. We consider a stochastic setting where the measurement matrices obtained at each phase are independent samples of a sub Gaussian random matrix. We prove that if a certain dynamic sample complexity that depends on the sizes of the measurement matrices at each phase, along with their duration and the number of phases, satisfy certain lower bound, the estimation error of SIHT over a fixed time horizon decays rapidly. Interestingly, this bound reveals that the probability of decay of estimation error is hardly affected even if very small number measurements are sporadically used in different phases. This theoretical observation is also corroborated using numerical experiments demonstrating that SIHT enjoys improved probability of recovery compared to offline IHT.
Online Caching with Optimal Switching Regret
Jan 18, 2021


Abstract:We consider the classical uncoded caching problem from an online learning point-of-view. A cache of limited storage capacity can hold $C$ files at a time from a large catalog. A user requests an arbitrary file from the catalog at each time slot. Before the file request from the user arrives, a caching policy populates the cache with any $C$ files of its choice. In the case of a cache-hit, the policy receives a unit reward and zero rewards otherwise. In addition to that, there is a cost associated with fetching files to the cache, which we refer to as the switching cost. The objective is to design a caching policy that incurs minimal regret while considering both the rewards due to cache-hits and the switching cost due to the file fetches. The main contribution of this paper is the switching regret analysis of a Follow the Perturbed Leader-based anytime caching policy, which is shown to have an order optimal switching regret. In this pursuit, we improve the best-known switching regret bound for this problem by a factor of $\Theta(\sqrt{C}).$ We conclude the paper by comparing the performance of different popular caching policies using a publicly available trace from a commercial CDN server.
A Two Stage Generalized Block Orthogonal Matching Pursuit (TSGBOMP) Algorithm
Aug 18, 2020



Abstract:Recovery of an unknown sparse signal from a few of its projections is the key objective of compressed sensing. Often one comes across signals that are not ordinarily sparse but are sparse blockwise. Existing block sparse recovery algorithms like BOMP make the assumption of uniform block size and known block boundaries, which are, however, not very practical in many applications. This paper addresses this problem and proposes a two step procedure, where the first stage is a coarse block location identification stage while the second stage carries out finer localization of a non-zero cluster within the window selected in the first stage. A detailed convergence analysis of the proposed algorithm is carried out by first defining the so-called pseudoblock-interleaved block RIP of the given generalized block sparse signal and then imposing upper bounds on the corresponding RIC. We also extend the analysis for complex vector as well as matrix entries where it turns out that the extension is non-trivial and requires special care. Furthermore, assuming real Gaussian sensing matrix entries, we find a lower bound on the probability that the derived recovery bounds are satisfied. The lower bound suggests that there are sets of parameters such that the derived bound is satisfied with high probability. Simulation results confirm significantly improved performance of the proposed algorithm as compared to BOMP.
Modified Hard Thresholding Pursuit with Regularization Assisted Support Identification
Jun 02, 2020


Abstract:Hard thresholding pursuit (HTP) is a recently proposed iterative sparse recovery algorithm which is a result of combination of a support selection step from iterated hard thresholding (IHT) and an estimation step from the orthogonal matching pursuit (OMP). HTP has been seen to enjoy improved recovery guarantee along with enhanced speed of convergence. Much of the success of HTP can be attributed to its improved support selection capability due to the support selection step from IHT. In this paper, we propose a generalized HTP algorithm, called regularized HTP (RHTP), where the support selection step of HTP is replaced by a IHT-type support selection where the cost function is replaced by a regularized cost function, while the estimation step continues to use the least squares function. With decomposable regularizer, satisfying certain regularity conditions, the RHTP algorithm is shown to produce a sequence dynamically equivalent to a sequence evolving according to a HTP-like evolution, where the identification stage has a gradient premultiplied with a time-varying diagonal matrix. RHTP is also proven, both theoretically, and numerically, to enjoy faster convergence vis-a-vis HTP with both noiseless and noisy measurement vectors.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge