A Two Stage Generalized Block Orthogonal Matching Pursuit (TSGBOMP) Algorithm

Recovery of an unknown sparse signal from a few of its projections is the key objective of compressed sensing. Often one comes across signals that are not ordinarily sparse but are sparse blockwise. Existing block sparse recovery algorithms like BOMP make the assumption of uniform block size and known block boundaries, which are, however, not very practical in many applications. This paper addresses this problem and proposes a two step procedure, where the first stage is a coarse block location identification stage while the second stage carries out finer localization of a non-zero cluster within the window selected in the first stage. A detailed convergence analysis of the proposed algorithm is carried out by first defining the so-called pseudoblock-interleaved block RIP of the given generalized block sparse signal and then imposing upper bounds on the corresponding RIC. We also extend the analysis for complex vector as well as matrix entries where it turns out that the extension is non-trivial and requires special care. Furthermore, assuming real Gaussian sensing matrix entries, we find a lower bound on the probability that the derived recovery bounds are satisfied. The lower bound suggests that there are sets of parameters such that the derived bound is satisfied with high probability. Simulation results confirm significantly improved performance of the proposed algorithm as compared to BOMP.

Modified Hard Thresholding Pursuit with Regularization Assisted Support Identification

Hard thresholding pursuit (HTP) is a recently proposed iterative sparse recovery algorithm which is a result of combination of a support selection step from iterated hard thresholding (IHT) and an estimation step from the orthogonal matching pursuit (OMP). HTP has been seen to enjoy improved recovery guarantee along with enhanced speed of convergence. Much of the success of HTP can be attributed to its improved support selection capability due to the support selection step from IHT. In this paper, we propose a generalized HTP algorithm, called regularized HTP (RHTP), where the support selection step of HTP is replaced by a IHT-type support selection where the cost function is replaced by a regularized cost function, while the estimation step continues to use the least squares function. With decomposable regularizer, satisfying certain regularity conditions, the RHTP algorithm is shown to produce a sequence dynamically equivalent to a sequence evolving according to a HTP-like evolution, where the identification stage has a gradient premultiplied with a time-varying diagonal matrix. RHTP is also proven, both theoretically, and numerically, to enjoy faster convergence vis-a-vis HTP with both noiseless and noisy measurement vectors.

Adaptive Combination of l0 LMS Adaptive Filters for Sparse System Identification in Fluctuating Noise Power

Recently, the l0-least mean square (l0-LMS) algorithm has been proposed to identify sparse linear systems by employing a sparsity-promoting continuous function as an approximation of l0 pseudonorm penalty. However, the performance of this algorithm is sensitive to the appropriate choice of the some parameter responsible for the zero-attracting intensity. The optimum choice for this parameter depends on the signal-to-noise ratio (SNR) prevailing in the system. Thus, it becomes difficult to fix a suitable value for this parameter, particularly in a situation where SNR fluctuates over time. In this work, we propose several adaptive combinations of differently parameterized l0-LMS to get an overall satisfactory performance independent of the SNR, and discuss some issues relevant to these combination structures. We also demonstrate an efficient partial update scheme which not only reduces the number of computations per iteration, but also achieves some interesting performance gain compared with the full update case. Then, we propose a new recursive least squares (RLS)-type rule to update the combining parameter more efficiently. Finally, we extend the combination of two filters to a combination of M number adaptive filters, which manifests further improvement for M > 2.

Performance Analysis of the Gradient Comparator LMS Algorithm

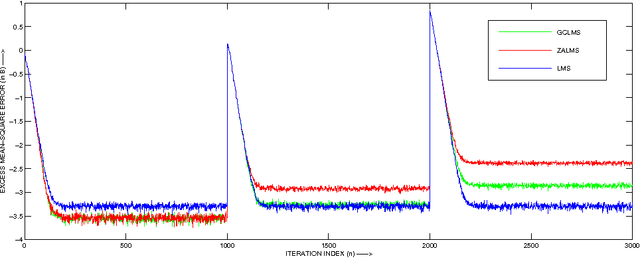
The sparsity-aware zero attractor least mean square (ZA-LMS) algorithm manifests much lower misadjustment in strongly sparse environment than its sparsity-agnostic counterpart, the least mean square (LMS), but is shown to perform worse than the LMS when sparsity of the impulse response decreases. The reweighted variant of the ZA-LMS, namely RZA-LMS shows robustness against this variation in sparsity, but at the price of increased computational complexity. The other variants such as the l 0 -LMS and the improved proportionate normalized LMS (IPNLMS), though perform satisfactorily, are also computationally intensive. The gradient comparator LMS (GC-LMS) is a practical solution of this trade-off when hardware constraint is to be considered. In this paper, we analyse the mean and the mean square convergence performance of the GC-LMS algorithm in detail. The analyses satisfactorily match with the simulation results.

Diffusion Adaptation Over Clustered Multitask Networks Based on the Affine Projection Algorithm

Distributed adaptive networks achieve better estimation performance by exploiting temporal and as well spatial diversity while consuming few resources. Recent works have studied the single task distributed estimation problem, in which the nodes estimate a single optimum parameter vector collaboratively. However, there are many important applications where the multiple vectors have to estimated simultaneously, in a collaborative manner. This paper presents multi-task diffusion strategies based on the Affine Projection Algorithm (APA), usage of APA makes the algorithm robust against the correlated input. The performance analysis of the proposed multi-task diffusion APA algorithm is studied in mean and mean square sense. And also a modified multi-task diffusion strategy is proposed that improves the performance in terms of convergence rate and steady state EMSE as well. Simulations are conducted to verify the analytical results.

Sparse Distributed Learning via Heterogeneous Diffusion Adaptive Networks

In-network distributed estimation of sparse parameter vectors via diffusion LMS strategies has been studied and investigated in recent years. In all the existing works, some convex regularization approach has been used at each node of the network in order to achieve an overall network performance superior to that of the simple diffusion LMS, albeit at the cost of increased computational overhead. In this paper, we provide analytical as well as experimental results which show that the convex regularization can be selectively applied only to some chosen nodes keeping rest of the nodes sparsity agnostic, while still enjoying the same optimum behavior as can be realized by deploying the convex regularization at all the nodes. Due to the incorporation of unregularized learning at a subset of nodes, less computational cost is needed in the proposed approach. We also provide a guideline for selection of the sparsity aware nodes and a closed form expression for the optimum regularization parameter.