Adaptive Combination of l0 LMS Adaptive Filters for Sparse System Identification in Fluctuating Noise Power

Recently, the l0-least mean square (l0-LMS) algorithm has been proposed to identify sparse linear systems by employing a sparsity-promoting continuous function as an approximation of l0 pseudonorm penalty. However, the performance of this algorithm is sensitive to the appropriate choice of the some parameter responsible for the zero-attracting intensity. The optimum choice for this parameter depends on the signal-to-noise ratio (SNR) prevailing in the system. Thus, it becomes difficult to fix a suitable value for this parameter, particularly in a situation where SNR fluctuates over time. In this work, we propose several adaptive combinations of differently parameterized l0-LMS to get an overall satisfactory performance independent of the SNR, and discuss some issues relevant to these combination structures. We also demonstrate an efficient partial update scheme which not only reduces the number of computations per iteration, but also achieves some interesting performance gain compared with the full update case. Then, we propose a new recursive least squares (RLS)-type rule to update the combining parameter more efficiently. Finally, we extend the combination of two filters to a combination of M number adaptive filters, which manifests further improvement for M > 2.

Performance Analysis of the Gradient Comparator LMS Algorithm

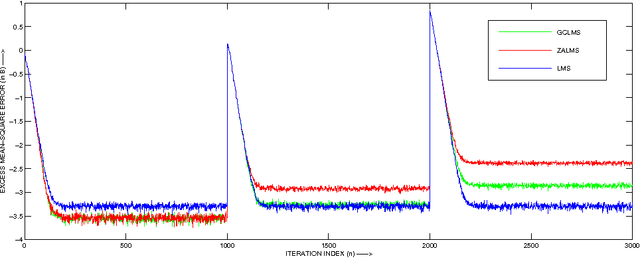
The sparsity-aware zero attractor least mean square (ZA-LMS) algorithm manifests much lower misadjustment in strongly sparse environment than its sparsity-agnostic counterpart, the least mean square (LMS), but is shown to perform worse than the LMS when sparsity of the impulse response decreases. The reweighted variant of the ZA-LMS, namely RZA-LMS shows robustness against this variation in sparsity, but at the price of increased computational complexity. The other variants such as the l 0 -LMS and the improved proportionate normalized LMS (IPNLMS), though perform satisfactorily, are also computationally intensive. The gradient comparator LMS (GC-LMS) is a practical solution of this trade-off when hardware constraint is to be considered. In this paper, we analyse the mean and the mean square convergence performance of the GC-LMS algorithm in detail. The analyses satisfactorily match with the simulation results.

Sparse Distributed Learning via Heterogeneous Diffusion Adaptive Networks

In-network distributed estimation of sparse parameter vectors via diffusion LMS strategies has been studied and investigated in recent years. In all the existing works, some convex regularization approach has been used at each node of the network in order to achieve an overall network performance superior to that of the simple diffusion LMS, albeit at the cost of increased computational overhead. In this paper, we provide analytical as well as experimental results which show that the convex regularization can be selectively applied only to some chosen nodes keeping rest of the nodes sparsity agnostic, while still enjoying the same optimum behavior as can be realized by deploying the convex regularization at all the nodes. Due to the incorporation of unregularized learning at a subset of nodes, less computational cost is needed in the proposed approach. We also provide a guideline for selection of the sparsity aware nodes and a closed form expression for the optimum regularization parameter.