Performance Analysis of the Gradient Comparator LMS Algorithm
Paper and Code
May 10, 2016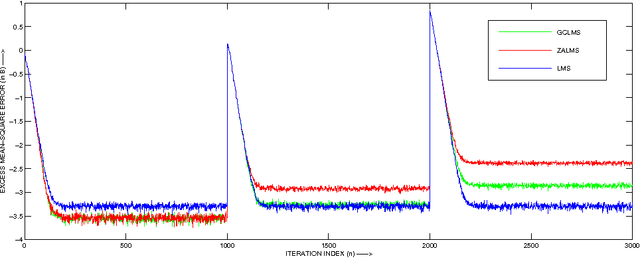

The sparsity-aware zero attractor least mean square (ZA-LMS) algorithm manifests much lower misadjustment in strongly sparse environment than its sparsity-agnostic counterpart, the least mean square (LMS), but is shown to perform worse than the LMS when sparsity of the impulse response decreases. The reweighted variant of the ZA-LMS, namely RZA-LMS shows robustness against this variation in sparsity, but at the price of increased computational complexity. The other variants such as the l 0 -LMS and the improved proportionate normalized LMS (IPNLMS), though perform satisfactorily, are also computationally intensive. The gradient comparator LMS (GC-LMS) is a practical solution of this trade-off when hardware constraint is to be considered. In this paper, we analyse the mean and the mean square convergence performance of the GC-LMS algorithm in detail. The analyses satisfactorily match with the simulation results.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge