$k\texttt{-experts}$ -- Online Policies and Fundamental Limits
Paper and Code
Oct 15, 2021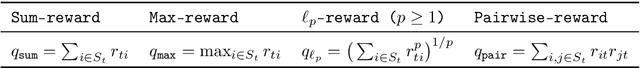
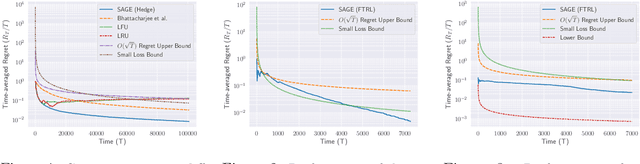

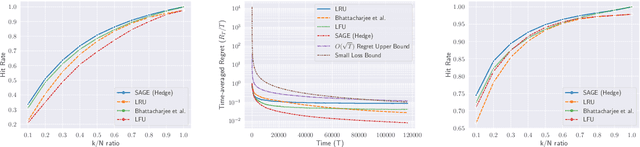
This paper introduces and studies the $k\texttt{-experts}$ problem -- a generalization of the classic Prediction with Expert's Advice (i.e., the $\texttt{Experts}$) problem. Unlike the $\texttt{Experts}$ problem, where the learner chooses exactly one expert, in this problem, the learner selects a subset of $k$ experts from a pool of $N$ experts at each round. The reward obtained by the learner at any round depends on the rewards of the selected experts. The $k\texttt{-experts}$ problem arises in many practical settings, including online ad placements, personalized news recommendations, and paging. Our primary goal is to design an online learning policy having a small regret. In this pursuit, we propose $\texttt{SAGE}$ ($\textbf{Sa}$mpled Hed$\textbf{ge}$) - a framework for designing efficient online learning policies by leveraging statistical sampling techniques. We show that, for many related problems, $\texttt{SAGE}$ improves upon the state-of-the-art bounds for regret and computational complexity. Furthermore, going beyond the notion of regret, we characterize the mistake bounds achievable by online learning policies for a class of stable loss functions. We conclude the paper by establishing a tight regret lower bound for a variant of the $k\texttt{-experts}$ problem and carrying out experiments with standard datasets.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge