Diagnostic Runtime Monitoring with Martingales

Machine learning systems deployed in safety-critical robotics settings must be robust to distribution shifts. However, system designers must understand the cause of a distribution shift in order to implement the appropriate intervention or mitigation strategy and prevent system failure. In this paper, we present a novel framework for diagnosing distribution shifts in a streaming fashion by deploying multiple stochastic martingales simultaneously. We show that knowledge of the underlying cause of a distribution shift can lead to proper interventions over the lifecycle of a deployed system. Our experimental framework can easily be adapted to different types of distribution shifts, models, and datasets. We find that our method outperforms existing work on diagnosing distribution shifts in terms of speed, accuracy, and flexibility, and validate the efficiency of our model in both simulated and live hardware settings.

A System-Level View on Out-of-Distribution Data in Robotics

When testing conditions differ from those represented in training data, so-called out-of-distribution (OOD) inputs can mar the reliability of black-box learned components in the modern robot autonomy stack. Therefore, coping with OOD data is an important challenge on the path towards trustworthy learning-enabled open-world autonomy. In this paper, we aim to demystify the topic of OOD data and its associated challenges in the context of data-driven robotic systems, drawing connections to emerging paradigms in the ML community that study the effect of OOD data on learned models in isolation. We argue that as roboticists, we should reason about the overall system-level competence of a robot as it performs tasks in OOD conditions. We highlight key research questions around this system-level view of OOD problems to guide future research toward safe and reliable learning-enabled autonomy.

Online Distribution Shift Detection via Recency Prediction

When deploying modern machine learning-enabled robotic systems in high-stakes applications, detecting distribution shift is critical. However, most existing methods for detecting distribution shift are not well-suited to robotics settings, where data often arrives in a streaming fashion and may be very high-dimensional. In this work, we present an online method for detecting distribution shift with guarantees on the false positive rate - i.e., when there is no distribution shift, our system is very unlikely (with probability $< \epsilon$) to falsely issue an alert; any alerts that are issued should therefore be heeded. Our method is specifically designed for efficient detection even with high dimensional data, and it empirically achieves up to 11x faster detection on realistic robotics settings compared to prior work while maintaining a low false negative rate in practice (whenever there is a distribution shift in our experiments, our method indeed emits an alert).

Sample-Efficient Safety Assurances using Conformal Prediction

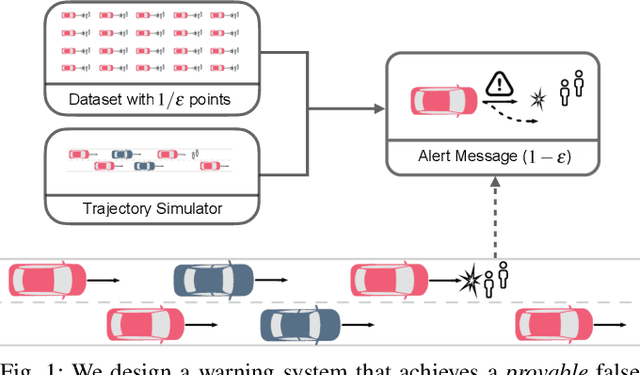
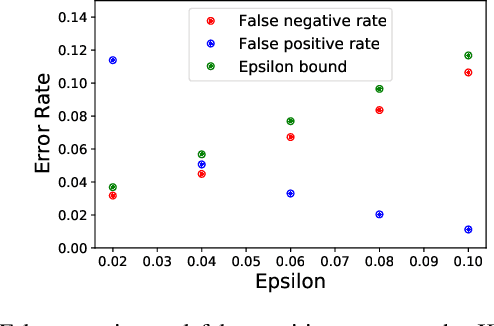
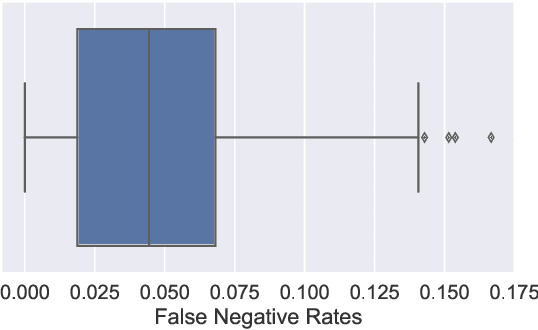
When deploying machine learning models in high-stakes robotics applications, the ability to detect unsafe situations is crucial. Early warning systems can provide alerts when an unsafe situation is imminent (in the absence of corrective action). To reliably improve safety, these warning systems should have a provable false negative rate; i.e. of the situations that are unsafe, fewer than $\epsilon$ will occur without an alert. In this work, we present a framework that combines a statistical inference technique known as conformal prediction with a simulator of robot/environment dynamics, in order to tune warning systems to provably achieve an $\epsilon$ false negative rate using as few as $1/\epsilon$ data points. We apply our framework to a driver warning system and a robotic grasping application, and empirically demonstrate guaranteed false negative rate and low false detection (positive) rate using very little data.

Localized Calibration: Metrics and Recalibration

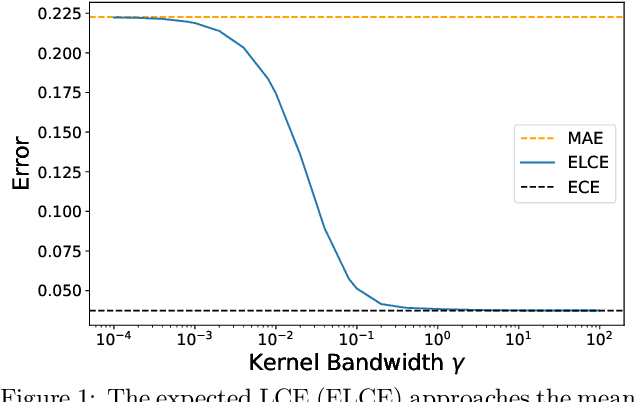
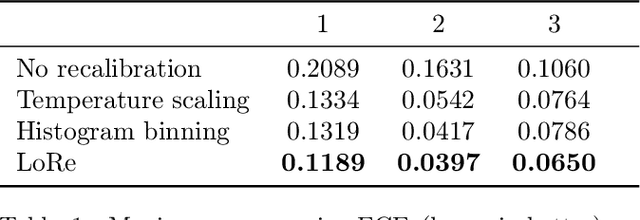
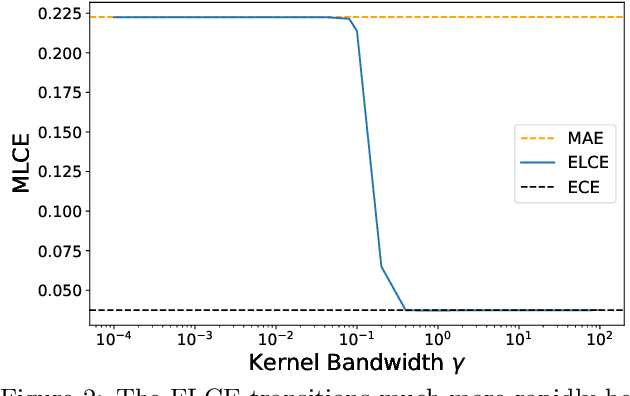
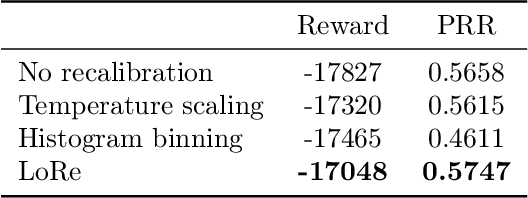
Probabilistic classifiers output confidence scores along with their predictions, and these confidence scores must be well-calibrated (i.e. reflect the true probability of an event) to be meaningful and useful for downstream tasks. However, existing metrics for measuring calibration are insufficient. Commonly used metrics such as the expected calibration error (ECE) only measure global trends, making them ineffective for measuring the calibration of a particular sample or subgroup. At the other end of the spectrum, a fully individualized calibration error is in general intractable to estimate from finite samples. In this work, we propose the local calibration error (LCE), a fine-grained calibration metric that spans the gap between fully global and fully individualized calibration. The LCE leverages learned features to automatically capture rich subgroups, and it measures the calibration error around each individual example via a similarity function. We then introduce a localized recalibration method, LoRe, that improves the LCE better than existing recalibration methods. Finally, we show that applying our recalibration method improves decision-making on downstream tasks.

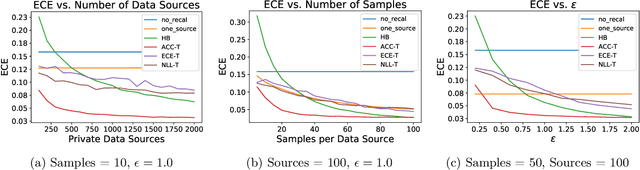
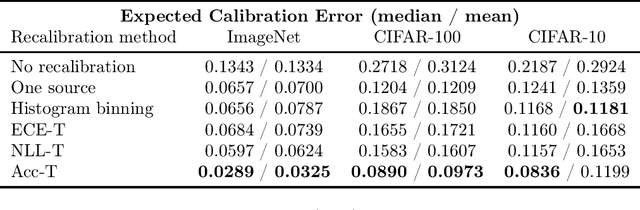
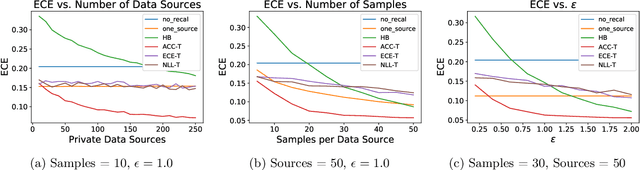
Privacy Preserving Recalibration under Domain Shift

Classifiers deployed in high-stakes real-world applications must output calibrated confidence scores, i.e. their predicted probabilities should reflect empirical frequencies. Recalibration algorithms can greatly improve a model's probability estimates; however, existing algorithms are not applicable in real-world situations where the test data follows a different distribution from the training data, and privacy preservation is paramount (e.g. protecting patient records). We introduce a framework that abstracts out the properties of recalibration problems under differential privacy constraints. This framework allows us to adapt existing recalibration algorithms to satisfy differential privacy while remaining effective for domain-shift situations. Guided by our framework, we also design a novel recalibration algorithm, accuracy temperature scaling, that outperforms prior work on private datasets. In an extensive empirical study, we find that our algorithm improves calibration on domain-shift benchmarks under the constraints of differential privacy. On the 15 highest severity perturbations of the ImageNet-C dataset, our method achieves a median ECE of 0.029, over 2x better than the next best recalibration method and almost 5x better than without recalibration.

Belief Propagation Neural Networks

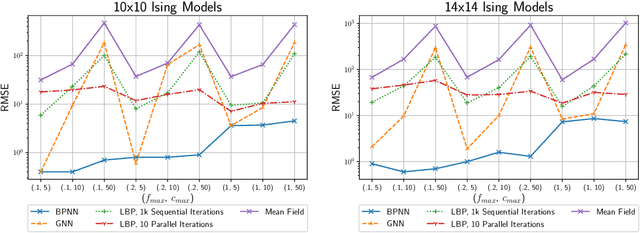
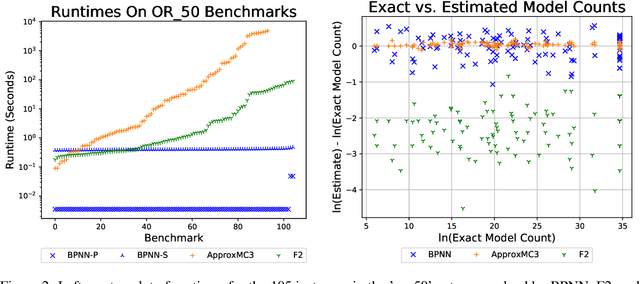
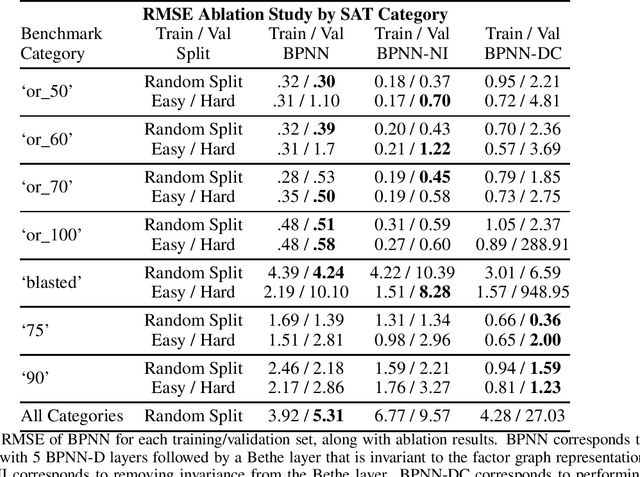
Learned neural solvers have successfully been used to solve combinatorial optimization and decision problems. More general counting variants of these problems, however, are still largely solved with hand-crafted solvers. To bridge this gap, we introduce belief propagation neural networks (BPNNs), a class of parameterized operators that operate on factor graphs and generalize Belief Propagation (BP). In its strictest form, a BPNN layer (BPNN-D) is a learned iterative operator that provably maintains many of the desirable properties of BP for any choice of the parameters. Empirically, we show that by training BPNN-D learns to perform the task better than the original BP: it converges 1.7x faster on Ising models while providing tighter bounds. On challenging model counting problems, BPNNs compute estimates 100's of times faster than state-of-the-art handcrafted methods, while returning an estimate of comparable quality.