Diagnostic Runtime Monitoring with Martingales

Machine learning systems deployed in safety-critical robotics settings must be robust to distribution shifts. However, system designers must understand the cause of a distribution shift in order to implement the appropriate intervention or mitigation strategy and prevent system failure. In this paper, we present a novel framework for diagnosing distribution shifts in a streaming fashion by deploying multiple stochastic martingales simultaneously. We show that knowledge of the underlying cause of a distribution shift can lead to proper interventions over the lifecycle of a deployed system. Our experimental framework can easily be adapted to different types of distribution shifts, models, and datasets. We find that our method outperforms existing work on diagnosing distribution shifts in terms of speed, accuracy, and flexibility, and validate the efficiency of our model in both simulated and live hardware settings.

Equivariant Neural Network for Factor Graphs

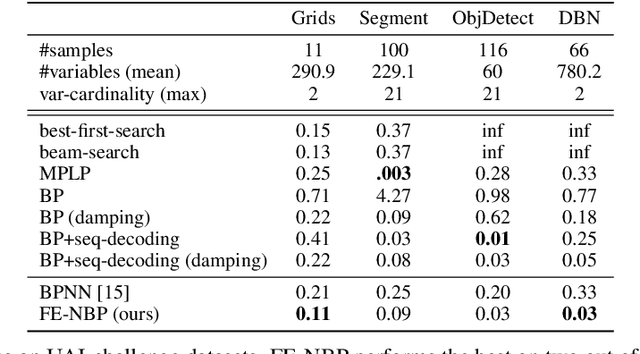
Several indices used in a factor graph data structure can be permuted without changing the underlying probability distribution. An algorithm that performs inference on a factor graph should ideally be equivariant or invariant to permutations of global indices of nodes, variable orderings within a factor, and variable assignment orderings. However, existing neural network-based inference procedures fail to take advantage of this inductive bias. In this paper, we precisely characterize these isomorphic properties of factor graphs and propose two inference models: Factor-Equivariant Neural Belief Propagation (FE-NBP) and Factor-Equivariant Graph Neural Networks (FE-GNN). FE-NBP is a neural network that generalizes BP and respects each of the above properties of factor graphs while FE-GNN is an expressive GNN model that relaxes an isomorphic property in favor of greater expressivity. Empirically, we demonstrate on both real-world and synthetic datasets, for both marginal inference and MAP inference, that FE-NBP and FE-GNN together cover a range of sample complexity regimes: FE-NBP achieves state-of-the-art performance on small datasets while FE-GNN achieves state-of-the-art performance on large datasets.

Sample-Efficient Safety Assurances using Conformal Prediction

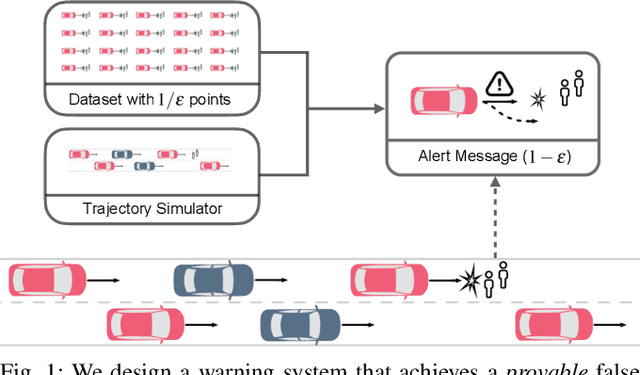
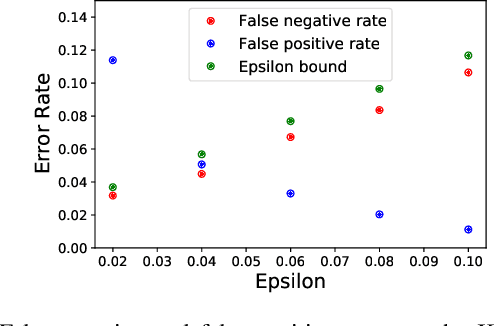
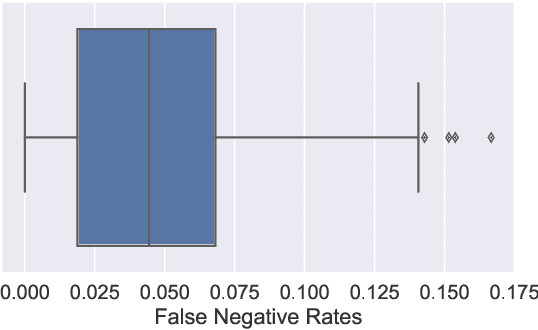
When deploying machine learning models in high-stakes robotics applications, the ability to detect unsafe situations is crucial. Early warning systems can provide alerts when an unsafe situation is imminent (in the absence of corrective action). To reliably improve safety, these warning systems should have a provable false negative rate; i.e. of the situations that are unsafe, fewer than $\epsilon$ will occur without an alert. In this work, we present a framework that combines a statistical inference technique known as conformal prediction with a simulator of robot/environment dynamics, in order to tune warning systems to provably achieve an $\epsilon$ false negative rate using as few as $1/\epsilon$ data points. We apply our framework to a driver warning system and a robotic grasping application, and empirically demonstrate guaranteed false negative rate and low false detection (positive) rate using very little data.

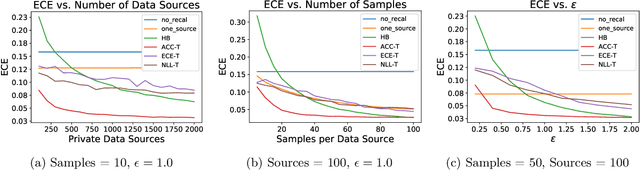
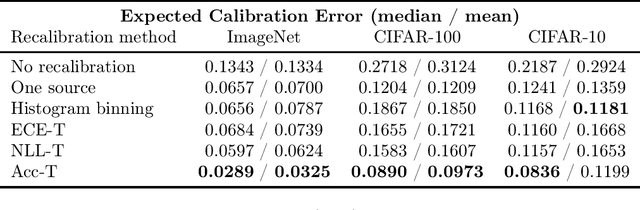
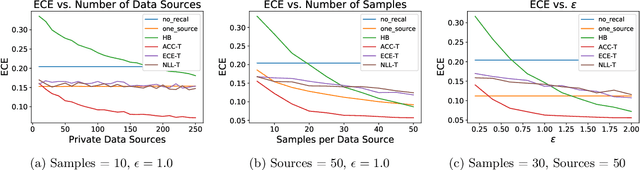
Privacy Preserving Recalibration under Domain Shift

Classifiers deployed in high-stakes real-world applications must output calibrated confidence scores, i.e. their predicted probabilities should reflect empirical frequencies. Recalibration algorithms can greatly improve a model's probability estimates; however, existing algorithms are not applicable in real-world situations where the test data follows a different distribution from the training data, and privacy preservation is paramount (e.g. protecting patient records). We introduce a framework that abstracts out the properties of recalibration problems under differential privacy constraints. This framework allows us to adapt existing recalibration algorithms to satisfy differential privacy while remaining effective for domain-shift situations. Guided by our framework, we also design a novel recalibration algorithm, accuracy temperature scaling, that outperforms prior work on private datasets. In an extensive empirical study, we find that our algorithm improves calibration on domain-shift benchmarks under the constraints of differential privacy. On the 15 highest severity perturbations of the ImageNet-C dataset, our method achieves a median ECE of 0.029, over 2x better than the next best recalibration method and almost 5x better than without recalibration.

Belief Propagation Neural Networks

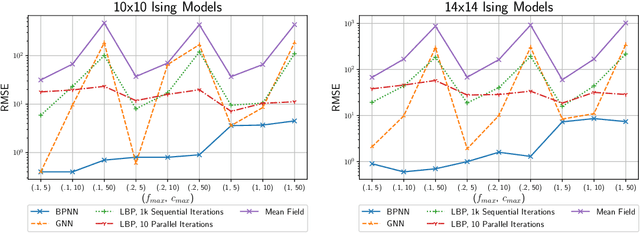
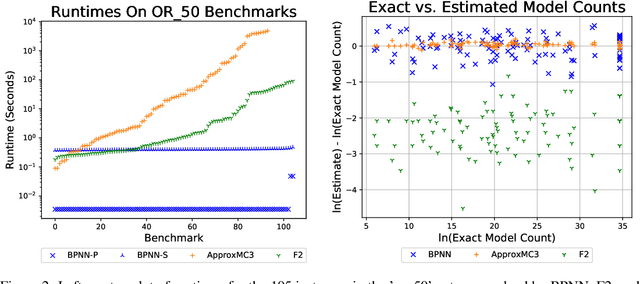
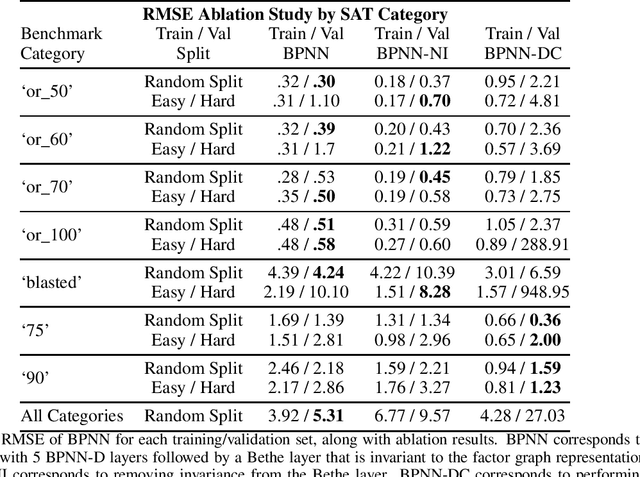
Learned neural solvers have successfully been used to solve combinatorial optimization and decision problems. More general counting variants of these problems, however, are still largely solved with hand-crafted solvers. To bridge this gap, we introduce belief propagation neural networks (BPNNs), a class of parameterized operators that operate on factor graphs and generalize Belief Propagation (BP). In its strictest form, a BPNN layer (BPNN-D) is a learned iterative operator that provably maintains many of the desirable properties of BP for any choice of the parameters. Empirically, we show that by training BPNN-D learns to perform the task better than the original BP: it converges 1.7x faster on Ising models while providing tighter bounds. On challenging model counting problems, BPNNs compute estimates 100's of times faster than state-of-the-art handcrafted methods, while returning an estimate of comparable quality.

Approximating the Permanent by Sampling from Adaptive Partitions

Computing the permanent of a non-negative matrix is a core problem with practical applications ranging from target tracking to statistical thermodynamics. However, this problem is also #P-complete, which leaves little hope for finding an exact solution that can be computed efficiently. While the problem admits a fully polynomial randomized approximation scheme, this method has seen little use because it is both inefficient in practice and difficult to implement. We present AdaPart, a simple and efficient method for drawing exact samples from an unnormalized distribution. Using AdaPart, we show how to construct tight bounds on the permanent which hold with high probability, with guaranteed polynomial runtime for dense matrices. We find that AdaPart can provide empirical speedups exceeding 25x over prior sampling methods on matrices that are challenging for variational based approaches. Finally, in the context of multi-target tracking, exact sampling from the distribution defined by the matrix permanent allows us to use the optimal proposal distribution during particle filtering. Using AdaPart, we show that this leads to improved tracking performance using an order of magnitude fewer samples.

Approximate Inference via Weighted Rademacher Complexity

Rademacher complexity is often used to characterize the learnability of a hypothesis class and is known to be related to the class size. We leverage this observation and introduce a new technique for estimating the size of an arbitrary weighted set, defined as the sum of weights of all elements in the set. Our technique provides upper and lower bounds on a novel generalization of Rademacher complexity to the weighted setting in terms of the weighted set size. This generalizes Massart's Lemma, a known upper bound on the Rademacher complexity in terms of the unweighted set size. We show that the weighted Rademacher complexity can be estimated by solving a randomly perturbed optimization problem, allowing us to derive high-probability bounds on the size of any weighted set. We apply our method to the problems of calculating the partition function of an Ising model and computing propositional model counts (#SAT). Our experiments demonstrate that we can produce tighter bounds than competing methods in both the weighted and unweighted settings.