Shushman Choudhury
Mobility-Embedded POIs: Learning What A Place Is and How It Is Used from Human Movement
Jan 29, 2026Abstract:Recent progress in geospatial foundation models highlights the importance of learning general-purpose representations for real-world locations, particularly points-of-interest (POIs) where human activity concentrates. Existing approaches, however, focus primarily on place identity derived from static textual metadata, or learn representations tied to trajectory context, which capture movement regularities rather than how places are actually used (i.e., POI's function). We argue that POI function is a missing but essential signal for general POI representations. We introduce Mobility-Embedded POIs (ME-POIs), a framework that augments POI embeddings derived, from language models with large-scale human mobility data to learn POI-centric, context-independent representations grounded in real-world usage. ME-POIs encodes individual visits as temporally contextualized embeddings and aligns them with learnable POI representations via contrastive learning to capture usage patterns across users and time. To address long-tail sparsity, we propose a novel mechanism that propagates temporal visit patterns from nearby, frequently visited POIs across multiple spatial scales. We evaluate ME-POIs on five newly proposed map enrichment tasks, testing its ability to capture both the identity and function of POIs. Across all tasks, augmenting text-based embeddings with ME-POIs consistently outperforms both text-only and mobility-only baselines. Notably, ME-POIs trained on mobility data alone can surpass text-only models on certain tasks, highlighting that POI function is a critical component of accurate and generalizable POI representations.
Scalable Learning of Segment-Level Traffic Congestion Functions
May 09, 2024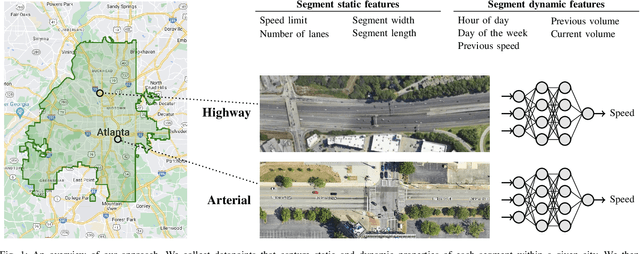
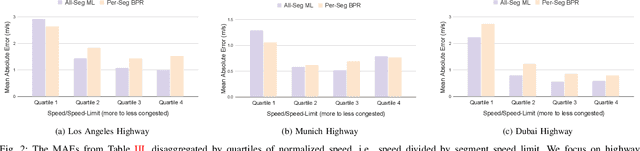
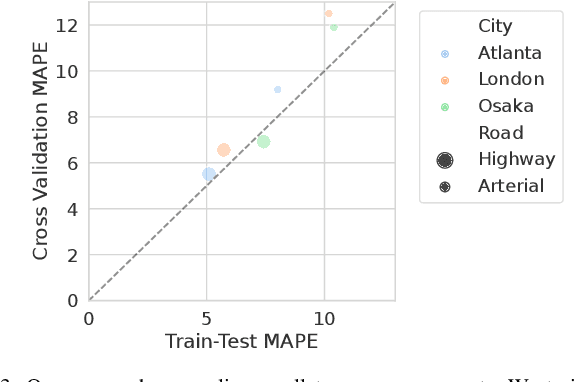
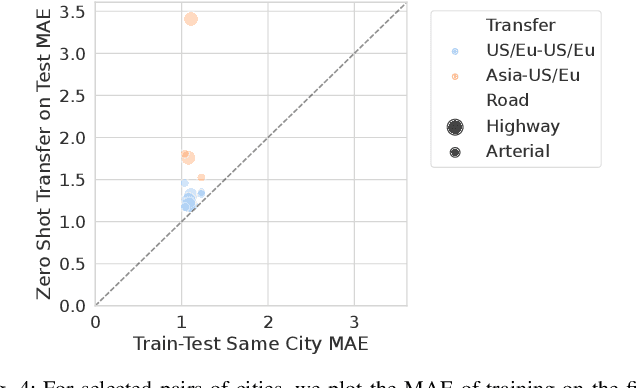
Abstract:We propose and study a data-driven framework for identifying traffic congestion functions (numerical relationships between observations of macroscopic traffic variables) at global scale and segment-level granularity. In contrast to methods that estimate a separate set of parameters for each roadway, ours learns a single black-box function over all roadways in a metropolitan area. First, we pool traffic data from all segments into one dataset, combining static attributes with dynamic time-dependent features. Second, we train a feed-forward neural network on this dataset, which we can then use on any segment in the area. We evaluate how well our framework identifies congestion functions on observed segments and how it generalizes to unobserved segments and predicts segment attributes on a large dataset covering multiple cities worldwide. For identification error on observed segments, our single data-driven congestion function compares favorably to segment-specific model-based functions on highway roads, but has room to improve on arterial roads. For generalization, our approach shows strong performance across cities and road types: both on unobserved segments in the same city and on zero-shot transfer learning between cities. Finally, for predicting segment attributes, we find that our approach can approximate critical densities for individual segments using their static properties.
Coordinated Multi-Agent Pathfinding for Drones and Trucks over Road Networks
Oct 17, 2021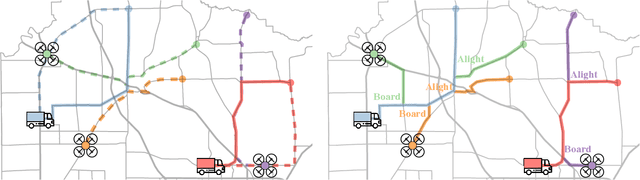
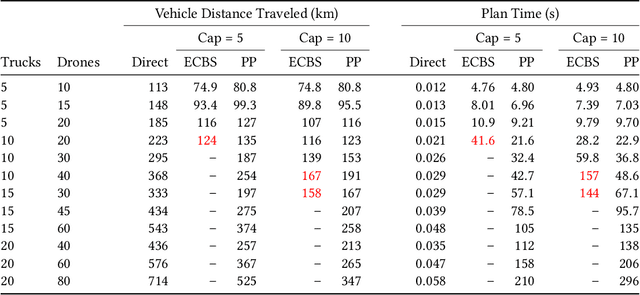
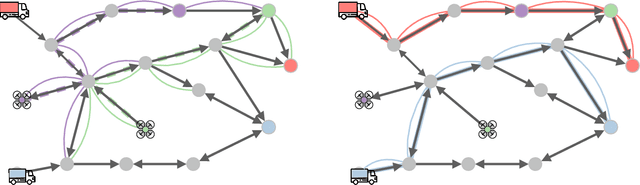
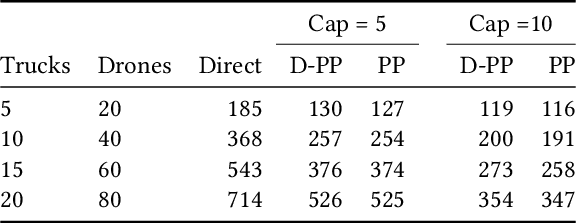
Abstract:We address the problem of routing a team of drones and trucks over large-scale urban road networks. To conserve their limited flight energy, drones can use trucks as temporary modes of transit en route to their own destinations. Such coordination can yield significant savings in total vehicle distance traveled, i.e., truck travel distance and drone flight distance, compared to operating drones and trucks independently. But it comes at the potentially prohibitive computational cost of deciding which trucks and drones should coordinate and when and where it is most beneficial to do so. We tackle this fundamental trade-off by decoupling our overall intractable problem into tractable sub-problems that we solve stage-wise. The first stage solves only for trucks, by computing paths that make them more likely to be useful transit options for drones. The second stage solves only for drones, by routing them over a composite of the road network and the transit network defined by truck paths from the first stage. We design a comprehensive algorithmic framework that frames each stage as a multi-agent path-finding problem and implement two distinct methods for solving them. We evaluate our approach on extensive simulations with up to $100$ agents on the real-world Manhattan road network containing nearly $4500$ vertices and $10000$ edges. Our framework saves on more than $50\%$ of vehicle distance traveled compared to independently solving for trucks and drones, and computes solutions for all settings within $5$ minutes on commodity hardware.
Scalable Anytime Planning for Multi-Agent MDPs
Jan 12, 2021
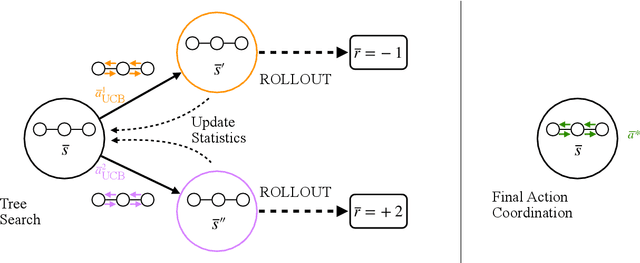

Abstract:We present a scalable tree search planning algorithm for large multi-agent sequential decision problems that require dynamic collaboration. Teams of agents need to coordinate decisions in many domains, but naive approaches fail due to the exponential growth of the joint action space with the number of agents. We circumvent this complexity through an anytime approach that allows us to trade computation for approximation quality and also dynamically coordinate actions. Our algorithm comprises three elements: online planning with Monte Carlo Tree Search (MCTS), factored representations of local agent interactions with coordination graphs, and the iterative Max-Plus method for joint action selection. We evaluate our approach on the benchmark SysAdmin domain with static coordination graphs and achieve comparable performance with much lower computation cost than our MCTS baselines. We also introduce a multi-drone delivery domain with dynamic, i.e., state-dependent coordination graphs, and demonstrate how our approach scales to large problems on this domain that are intractable for other MCTS methods. We provide an open-source implementation of our algorithm at https://github.com/JuliaPOMDP/FactoredValueMCTS.jl.
Dynamic Multi-Robot Task Allocation under Uncertainty and Temporal Constraints
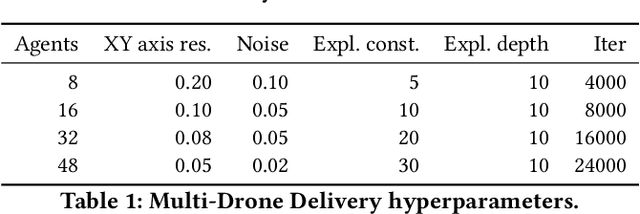
May 29, 2020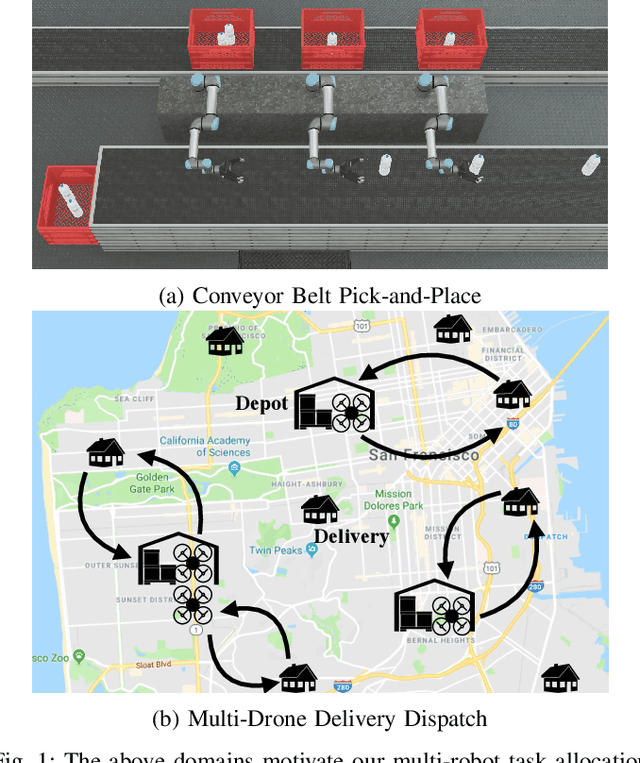
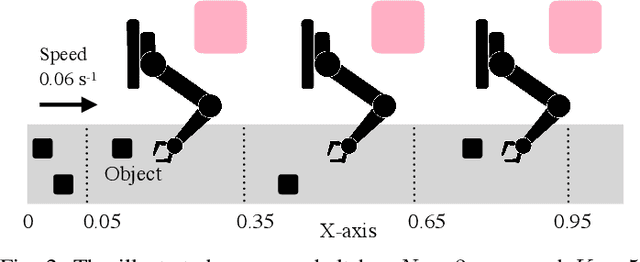
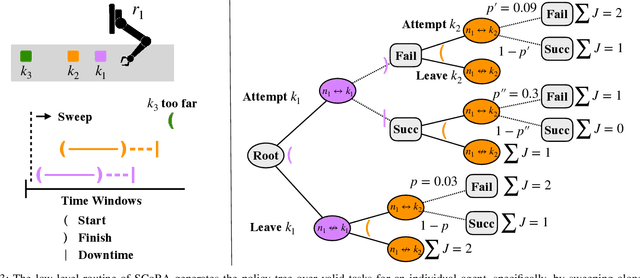
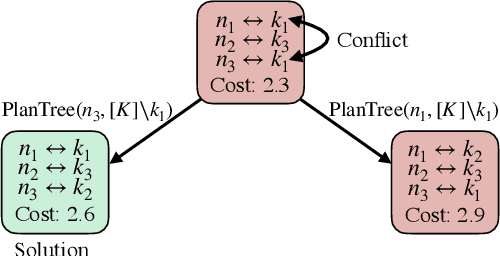
Abstract:We consider the problem of dynamically allocating tasks to multiple agents under time window constraints and task completion uncertainty. Our objective is to minimize the number of unsuccessful tasks at the end of the operation horizon. We present a multi-robot allocation algorithm that decouples the key computational challenges of sequential decision-making under uncertainty and multi-agent coordination and addresses them in a hierarchical manner. The lower layer computes policies for individual agents using dynamic programming with tree search, and the upper layer resolves conflicts in individual plans to obtain a valid multi-agent allocation. Our algorithm, Stochastic Conflict-Based Allocation (SCoBA), is optimal in expectation and complete under some reasonable assumptions. In practice, SCoBA is computationally efficient enough to interleave planning and execution online. On the metric of successful task completion, SCoBA consistently outperforms a number of baseline methods and shows strong competitive performance against an oracle with complete lookahead. It also scales well with the number of tasks and agents. We validate our results over a wide range of simulations on two distinct domains: multi-arm conveyor belt pick-and-place and multi-drone delivery dispatch in a city.
Adaptive Informative Path Planning with Multimodal Sensing
Mar 21, 2020


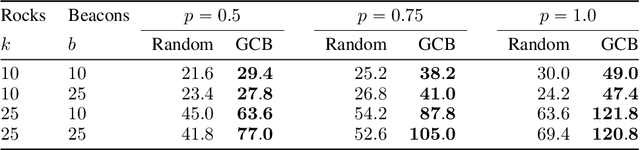
Abstract:Adaptive Informative Path Planning (AIPP) problems model an agent tasked with obtaining information subject to resource constraints in unknown, partially observable environments. Existing work on AIPP has focused on representing observations about the world as a result of agent movement. We formulate the more general setting where the agent may choose between different sensors at the cost of some energy, in addition to traversing the environment to gather information. We call this problem AIPPMS (MS for Multimodal Sensing). AIPPMS requires reasoning jointly about the effects of sensing and movement in terms of both energy expended and information gained. We frame AIPPMS as a Partially Observable Markov Decision Process (POMDP) and solve it with online planning. Our approach is based on the Partially Observable Monte Carlo Planning framework with modifications to ensure constraint feasibility and a heuristic rollout policy tailored for AIPPMS. We evaluate our method on two domains: a simulated search-and-rescue scenario and a challenging extension to the classic RockSample problem. We find that our approach outperforms a classic AIPP algorithm that is modified for AIPPMS, as well as online planning using a random rollout policy.
Efficient Large-Scale Multi-Drone Delivery Using Transit Networks
Sep 26, 2019



Abstract:We consider the problem of controlling a large fleet of drones to deliver packages simultaneously across broad urban areas. To conserve their limited flight range, drones can seamlessly hop between and ride on top of public transit vehicles (e.g., buses and trams). We design a novel comprehensive algorithmic framework that strives to minimize the maximum time to complete any delivery. We address the multifaceted complexity of the problem through a two-layer approach. First, the upper layer assigns drones to package delivery sequences with a provably near-optimal polynomial-time task allocation algorithm. Then, the lower layer executes the allocation by periodically routing the fleet over the transit network while employing efficient bounded-suboptimal multi-agent pathfinding techniques tailored to our setting. We present extensive experiments supporting the efficiency of our approach on settings with up to $200$ drones, $5000$ packages, and large transit networks of up to $8000$ stops in San Francisco and the Washington DC area. Our results show that the framework can compute solutions within a few seconds (up to $2$ minutes for the largest settings) on commodity hardware, and that drones travel up to $450 \%$ of their flight range by using public transit.
Hybrid Planning for Dynamic Multimodal Stochastic Shortest Paths
Jun 21, 2019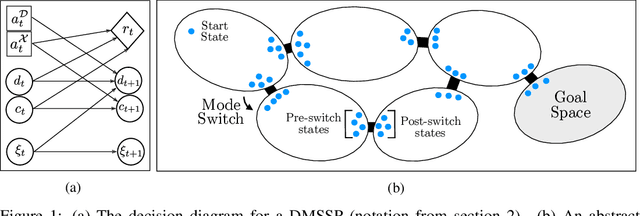


Abstract:Sequential decision problems in applications such as manipulation in warehouses, multi-step meal preparation, and routing in autonomous vehicle networks often involve reasoning about uncertainty, planning over discrete modes as well as continuous states, and reacting to dynamic updates. To formalize such problems generally, we introduce a class of Markov Decision Processes (MDPs) called Dynamic Multimodal Stochastic Shortest Paths (DMSSPs). Much of the work in these domains solves deterministic variants, which can yield poor results when the uncertainty has downstream effects. We develop a Hybrid Stochastic Planning (HSP) algorithm, which uses domain-agnostic abstractions to efficiently unify heuristic search for planning over discrete modes, approximate dynamic programming for stochastic planning over continuous states, and hierarchical interleaved planning and execution. In the domain of autonomous multimodal routing, HSP obtains significantly higher quality solutions than a state-of-the-art Upper Confidence Trees algorithm and a two-level Receding Horizon Control algorithm.
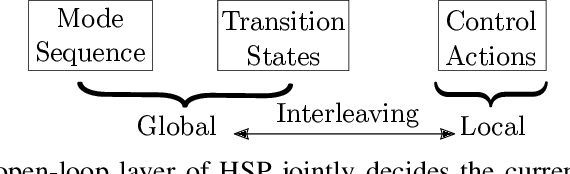
Dynamic Real-time Multimodal Routing with Hierarchical Hybrid Planning
Feb 05, 2019



Abstract:We introduce the problem of Dynamic Real-time Multimodal Routing (DREAMR), which requires planning and executing routes under uncertainty for an autonomous agent. The agent has access to a time-varying transit vehicle network in which it can use multiple modes of transportation. For instance, a drone can either fly or ride on terrain vehicles for segments of their routes. DREAMR is a difficult problem of sequential decision making under uncertainty with both discrete and continuous variables. We design a novel hierarchical hybrid planning framework to solve the DREAMR problem that exploits its structural decomposability. Our framework consists of a global open-loop planning layer that invokes and monitors a local closed-loop execution layer. Additional abstractions allow efficient and seamless interleaving of planning and execution. We create a large-scale simulation for DREAMR problems, with each scenario having hundreds of transportation routes and thousands of connection points. Our algorithmic framework significantly outperforms a receding horizon control baseline, in terms of elapsed time to reach the destination and energy expended by the agent.
Anytime Motion Planning on Large Dense Roadmaps with Expensive Edge Evaluations
Nov 10, 2017

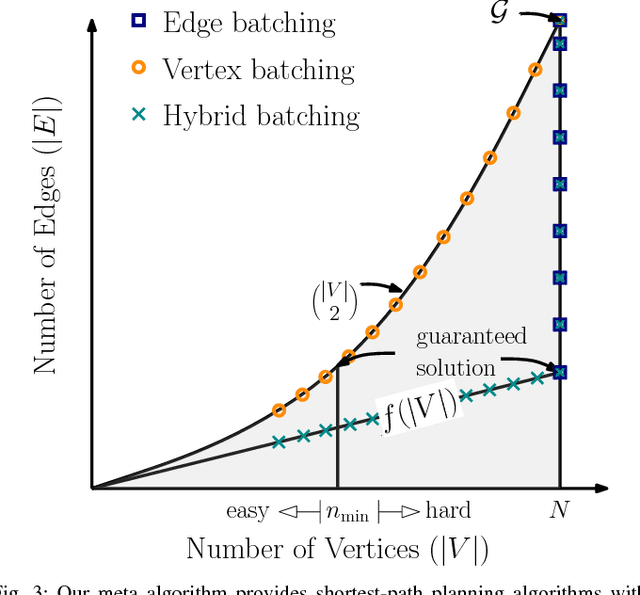
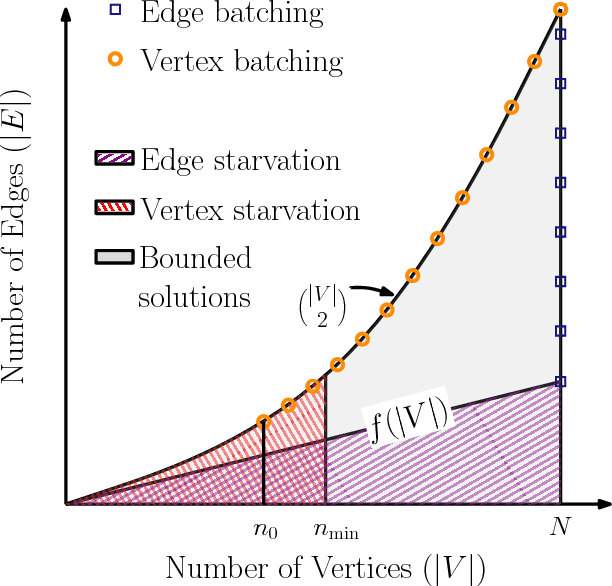
Abstract:We propose an algorithmic framework for efficient anytime motion planning on large dense geometric roadmaps, in domains where collision checks and therefore edge evaluations are computationally expensive. A large dense roadmap (graph) can typically ensure the existence of high quality solutions for most motion-planning problems, but the size of the roadmap, particularly in high-dimensional spaces, makes existing search-based planning algorithms computationally expensive. We deal with the challenges of expensive search and collision checking in two ways. First, we frame the problem of anytime motion planning on roadmaps as searching for the shortest path over a sequence of subgraphs of the entire roadmap graph, generated by some densification strategy. This lets us achieve bounded sub-optimality with bounded worst-case planning effort. Second, for searching each subgraph, we develop an anytime planning algorithm which uses a belief model to compute the collision probability of unknown configurations and searches for paths that are Pareto-optimal in path length and collision probability. This algorithm is efficient with respect to collision checks as it searches for successively shorter paths. We theoretically analyze both our ideas and evaluate them individually on high-dimensional motion-planning problems. Finally, we apply both of these ideas together in our algorithmic framework for anytime motion planning, and show that it outperforms BIT* on high-dimensional hypercube problems.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge