Hybrid DDP in Clutter (CHDDP): Trajectory Optimization for Hybrid Dynamical System in Cluttered Environments
Paper and Code
Oct 14, 2017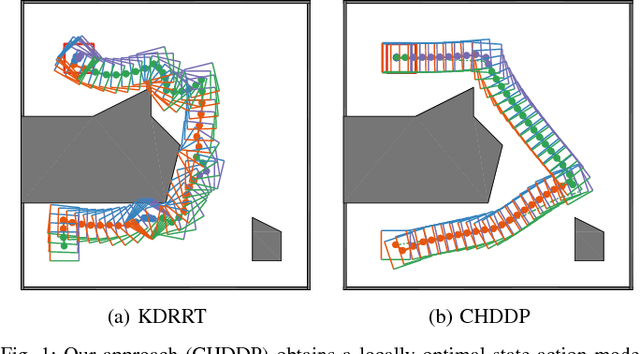
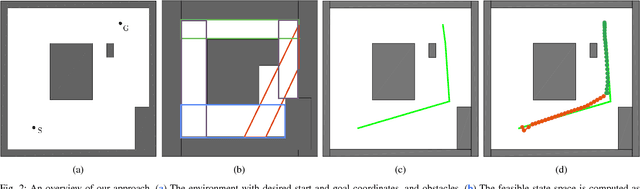
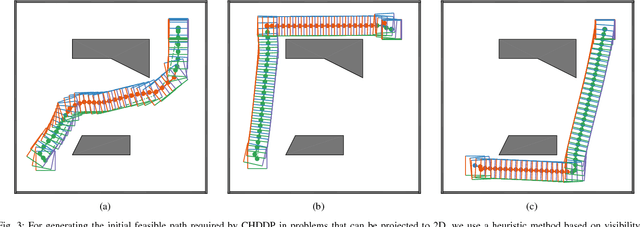
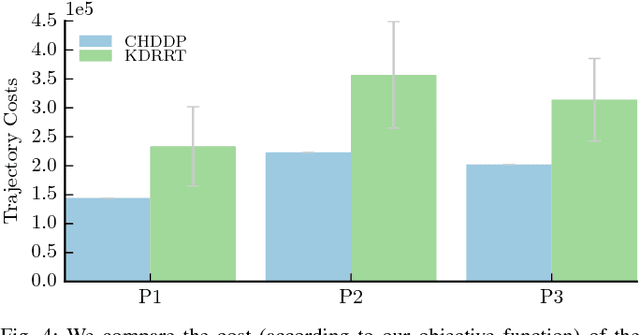
We present an algorithm for obtaining an optimal control policy for hybrid dynamical systems in cluttered environments. To the best of our knowledge, this is the first attempt to have a locally optimal solution for this specific problem setting. Our approach extends an optimal control algorithm for hybrid dynamical systems in the obstacle-free case to environments with obstacles. Our method does not require any preset mode sequence or heuristics to prune the exponential search of mode sequences. By first solving the relaxed problem of getting an obstacle-free, dynamically feasible trajectory and then solving for both obstacle-avoidance and optimality, we can generate smooth, locally optimal control policies. We demonstrate the performance of our algorithm on a box-pushing example in a number of environments against the baseline of randomly sampling modes and actions with a Kinodynamic RRT.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge