Hybrid Planning for Dynamic Multimodal Stochastic Shortest Paths
Paper and Code
Jun 21, 2019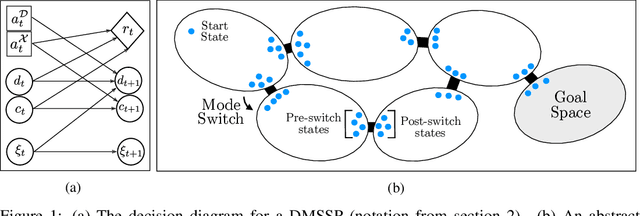

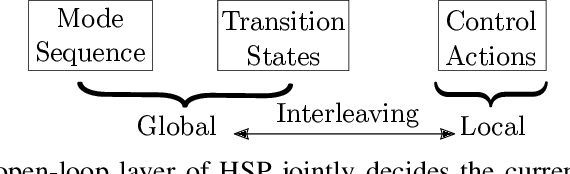

Sequential decision problems in applications such as manipulation in warehouses, multi-step meal preparation, and routing in autonomous vehicle networks often involve reasoning about uncertainty, planning over discrete modes as well as continuous states, and reacting to dynamic updates. To formalize such problems generally, we introduce a class of Markov Decision Processes (MDPs) called Dynamic Multimodal Stochastic Shortest Paths (DMSSPs). Much of the work in these domains solves deterministic variants, which can yield poor results when the uncertainty has downstream effects. We develop a Hybrid Stochastic Planning (HSP) algorithm, which uses domain-agnostic abstractions to efficiently unify heuristic search for planning over discrete modes, approximate dynamic programming for stochastic planning over continuous states, and hierarchical interleaved planning and execution. In the domain of autonomous multimodal routing, HSP obtains significantly higher quality solutions than a state-of-the-art Upper Confidence Trees algorithm and a two-level Receding Horizon Control algorithm.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge