Anytime Motion Planning on Large Dense Roadmaps with Expensive Edge Evaluations
Paper and Code
Nov 10, 2017

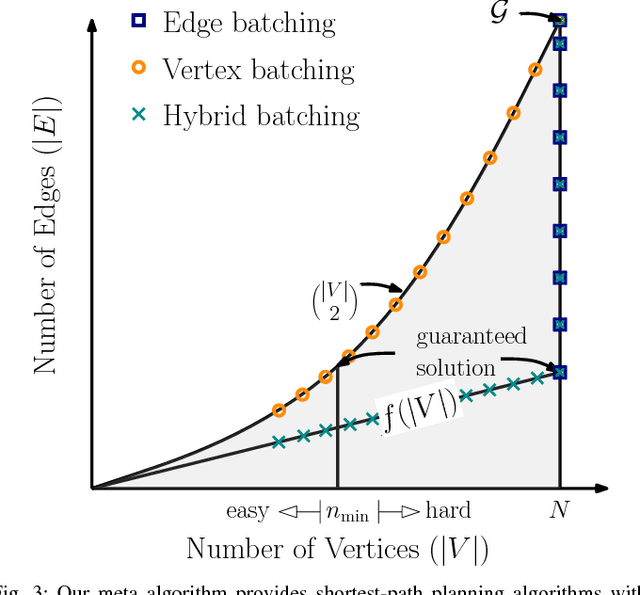
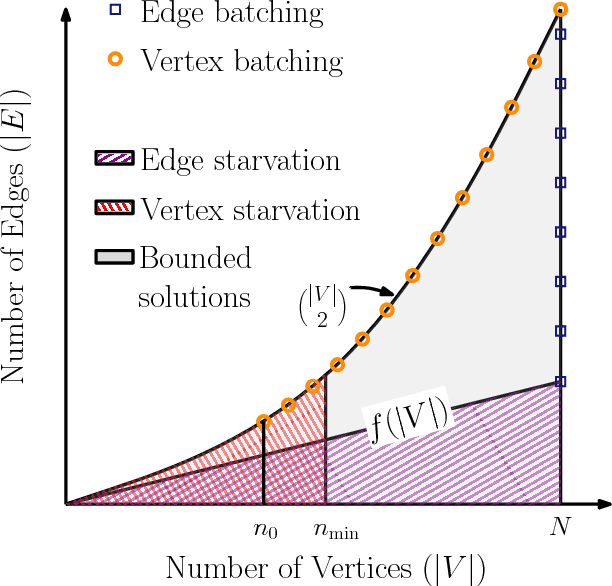
We propose an algorithmic framework for efficient anytime motion planning on large dense geometric roadmaps, in domains where collision checks and therefore edge evaluations are computationally expensive. A large dense roadmap (graph) can typically ensure the existence of high quality solutions for most motion-planning problems, but the size of the roadmap, particularly in high-dimensional spaces, makes existing search-based planning algorithms computationally expensive. We deal with the challenges of expensive search and collision checking in two ways. First, we frame the problem of anytime motion planning on roadmaps as searching for the shortest path over a sequence of subgraphs of the entire roadmap graph, generated by some densification strategy. This lets us achieve bounded sub-optimality with bounded worst-case planning effort. Second, for searching each subgraph, we develop an anytime planning algorithm which uses a belief model to compute the collision probability of unknown configurations and searches for paths that are Pareto-optimal in path length and collision probability. This algorithm is efficient with respect to collision checks as it searches for successively shorter paths. We theoretically analyze both our ideas and evaluate them individually on high-dimensional motion-planning problems. Finally, we apply both of these ideas together in our algorithmic framework for anytime motion planning, and show that it outperforms BIT* on high-dimensional hypercube problems.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge