Hardware-Accelerated Ray Tracing for Discrete and Continuous Collision Detection on GPUs

This paper presents a set of simple and intuitive robot collision detection algorithms that show substantial scaling improvements for high geometric complexity and large numbers of collision queries by leveraging hardware-accelerated ray tracing on GPUs. It is the first leveraging hardware-accelerated ray-tracing for direct volume mesh-to-mesh discrete collision detection and applying it to continuous collision detection. We introduce two methods: Ray-Traced Discrete-Pose Collision Detection for exact robot mesh to obstacle mesh collision detection, and Ray-Traced Continuous Collision Detection for robot sphere representation to obstacle mesh swept collision detection, using piecewise-linear or quadratic B-splines. For robot link meshes totaling 24k triangles and obstacle meshes of over 190k triangles, our methods were up to 3 times faster in batched discrete-pose queries than a state-of-the-art GPU-based method using a sphere robot representation. For the same obstacle mesh scene, our sphere-robot continuous collision detection was up to 9 times faster depending on trajectory batch size. We also performed a detailed measurement of the volume coverage accuracy of various sphere/mesh pose/path representations to provide insight into the tradeoffs between speed and accuracy of different robot collision detection methods.

Grasp Failure Constraints for Fast and Reliable Pick-and-Place Using Multi-Suction-Cup Grippers

Multi-suction-cup grippers are frequently employed to perform pick-and-place robotic tasks, especially in industrial settings where grasping a wide range of light to heavy objects in limited amounts of time is a common requirement. However, most existing works focus on using one or two suction cups to grasp only irregularly shaped but light objects. There is a lack of research on robust manipulation of heavy objects using larger arrays of suction cups, which introduces challenges in modeling and predicting grasp failure. This paper presents a general approach to modeling grasp strength in multi-suction-cup grippers, introducing new constraints usable for trajectory planning and optimization to achieve fast and reliable pick-and-place maneuvers. The primary modeling challenge is the accurate prediction of the distribution of loads at each suction cup while grasping objects. To solve for this load distribution, we find minimum spring potential energy configurations through a simple quadratic program. This results in a computationally efficient analytical solution that can be integrated to formulate grasp failure constraints in time-optimal trajectory planning. Finally, we present experimental results to validate the efficiency and accuracy of the proposed model.

On the Performance of Jerk-Constrained Time-Optimal Trajectory Planning for Industrial Manipulators

Jerk-constrained trajectories offer a wide range of advantages that collectively improve the performance of robotic systems, including increased energy efficiency, durability, and safety. In this paper, we present a novel approach to jerk-constrained time-optimal trajectory planning (TOTP), which follows a specified path while satisfying up to third-order constraints to ensure safety and smooth motion. One significant challenge in jerk-constrained TOTP is a non-convex formulation arising from the inclusion of third-order constraints. Approximating inequality constraints can be particularly challenging because the resulting solutions may violate the actual constraints. We address this problem by leveraging convexity within the proposed formulation to form conservative inequality constraints. We then obtain the desired trajectories by solving an $\boldsymbol n$-dimensional Sequential Linear Program (SLP) iteratively until convergence. Lastly, we evaluate in a real robot the performance of trajectories generated with and without jerk limits in terms of peak power, torque efficiency, and tracking capability.

Real-Time Model Predictive Control for Industrial Manipulators with Singularity-Tolerant Hierarchical Task Control

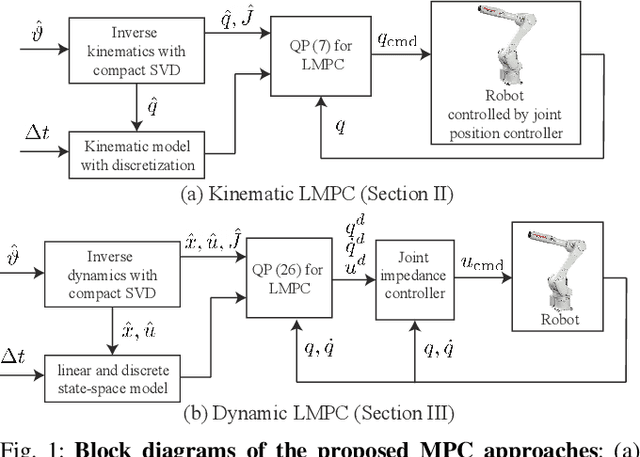
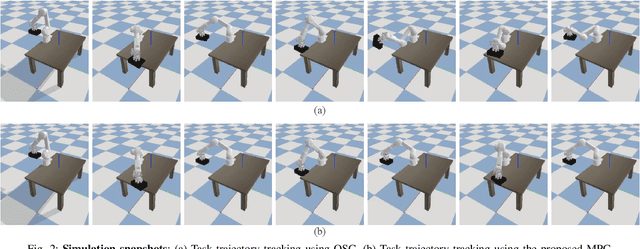
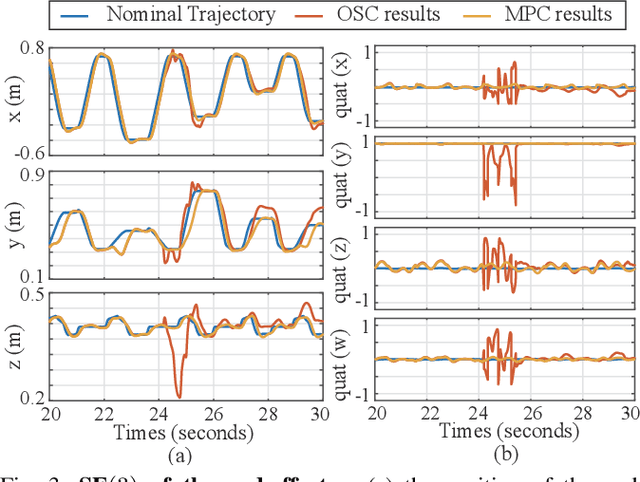
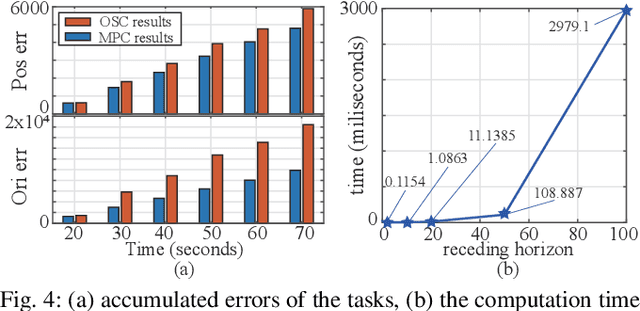
This paper proposes a real-time model predictive control (MPC) scheme to execute multiple tasks using robots over a finite-time horizon. In industrial robotic applications, we must carefully consider multiple constraints for avoiding joint position, velocity, and torque limits. In addition, singularity-free and smooth motions require executing tasks continuously and safely. Instead of formulating nonlinear MPC problems, we devise linear MPC problems using kinematic and dynamic models linearized along nominal trajectories produced by hierarchical controllers. These linear MPC problems are solvable via the use of Quadratic Programming; therefore, we significantly reduce the computation time of the proposed MPC framework so the resulting update frequency is higher than 1 kHz. Our proposed MPC framework is more efficient in reducing task tracking errors than a baseline based on operational space control (OSC). We validate our approach in numerical simulations and in real experiments using an industrial manipulator. More specifically, we deploy our method in two practical scenarios for robotic logistics: 1) controlling a robot carrying heavy payloads while accounting for torque limits, and 2) controlling the end-effector while avoiding singularities.

ReachBot: A Small Robot for Large Mobile Manipulation Tasks

Robots are widely deployed in space environments because of their versatility and robustness. However, adverse gravity conditions and challenging terrain geometry expose the limitations of traditional robot designs, which are often forced to sacrifice one of mobility or manipulation capabilities to attain the other. Prospective climbing operations in these environments reveals a need for small, compact robots capable of versatile mobility and manipulation. We propose a novel robotic concept called ReachBot that fills this need by combining two existing technologies: extendable booms and mobile manipulation. ReachBot leverages the reach and tensile strength of extendable booms to achieve an outsized reachable workspace and wrench capability. Through their lightweight, compactable structure, these booms also reduce mass and complexity compared to traditional rigid-link articulated-arm designs. Using these advantages, ReachBot excels in mobile manipulation missions in low gravity or that require climbing, particularly when anchor points are sparse. After introducing the ReachBot concept, we discuss modeling approaches and strategies for increasing stability and robustness. We then develop a 2D analytical model for ReachBot's dynamics inspired by grasp models for dexterous manipulators. Next, we introduce a waypoint-tracking controller for a planar ReachBot in microgravity. Our simulation results demonstrate the controller's robustness to disturbances and modeling error. Finally, we briefly discuss next steps that build on these initially promising results to realize the full potential of ReachBot.

Composable Geometric Motion Policies using Multi-Task Pullback Bundle Dynamical Systems

Despite decades of work in fast reactive planning and control, challenges remain in developing reactive motion policies on non-Euclidean manifolds and enforcing constraints while avoiding undesirable potential function local minima. This work presents a principled method for designing and fusing desired robot task behaviors into a stable robot motion policy, leveraging the geometric structure of non-Euclidean manifolds, which are prevalent in robot configuration and task spaces. Our Pullback Bundle Dynamical Systems (PBDS) framework drives desired task behaviors and prioritizes tasks using separate position-dependent and position/velocity-dependent Riemannian metrics, respectively, thus simplifying individual task design and modular composition of tasks. For enforcing constraints, we provide a class of metric-based tasks, eliminating local minima by imposing non-conflicting potential functions only for goal region attraction. We also provide a geometric optimization problem for combining tasks inspired by Riemannian Motion Policies (RMPs) that reduces to a simple least-squares problem, and we show that our approach is geometrically well-defined. We demonstrate the PBDS framework on the sphere $\mathbb S^2$ and at 300-500 Hz on a manipulator arm, and we provide task design guidance and an open-source Julia library implementation. Overall, this work presents a fast, easy-to-use framework for generating motion policies without unwanted potential function local minima on general manifolds.

Trajectory Optimization on Manifolds: A Theoretically-Guaranteed Embedded Sequential Convex Programming Approach

Sequential Convex Programming (SCP) has recently gained popularity as a tool for trajectory optimization due to its sound theoretical properties and practical performance. Yet, most SCP-based methods for trajectory optimization are restricted to Euclidean settings, which precludes their application to problem instances where one must reason about manifold-type constraints (that is, constraints, such as loop closure, which restrict the motion of a system to a subset of the ambient space). The aim of this paper is to fill this gap by extending SCP-based trajectory optimization methods to a manifold setting. The key insight is to leverage geometric embeddings to lift a manifold-constrained trajectory optimization problem into an equivalent problem defined over a space enjoying a Euclidean structure. This insight allows one to extend existing SCP methods to a manifold setting in a fairly natural way. In particular, we present a SCP algorithm for manifold problems with refined theoretical guarantees that resemble those derived for the Euclidean setting, and demonstrate its practical performance via numerical experiments.

GuSTO: Guaranteed Sequential Trajectory Optimization via Sequential Convex Programming

Sequential Convex Programming (SCP) has recently seen a surge of interest as a tool for trajectory optimization. However, most available methods lack rigorous performance guarantees and they are often tailored to specific optimal control setups. In this paper, we present GuSTO (Guaranteed Sequential Trajectory Optimization), an algorithmic framework to solve trajectory optimization problems for control-affine systems with drift. GuSTO generalizes earlier SCP-based methods for trajectory optimization (by addressing, for example, goal-set constraints and problems with either fixed or free final time) and enjoys theoretical convergence guarantees in terms of convergence to, at least, a stationary point. The theoretical analysis is further leveraged to devise an accelerated implementation of GuSTO, which originally infuses ideas from indirect optimal control into an SCP context. Numerical experiments on a variety of trajectory optimization setups show that GuSTO generally outperforms current state-of-the-art approaches in terms of success rates, solution quality, and computation times.