Grasp Failure Constraints for Fast and Reliable Pick-and-Place Using Multi-Suction-Cup Grippers

Multi-suction-cup grippers are frequently employed to perform pick-and-place robotic tasks, especially in industrial settings where grasping a wide range of light to heavy objects in limited amounts of time is a common requirement. However, most existing works focus on using one or two suction cups to grasp only irregularly shaped but light objects. There is a lack of research on robust manipulation of heavy objects using larger arrays of suction cups, which introduces challenges in modeling and predicting grasp failure. This paper presents a general approach to modeling grasp strength in multi-suction-cup grippers, introducing new constraints usable for trajectory planning and optimization to achieve fast and reliable pick-and-place maneuvers. The primary modeling challenge is the accurate prediction of the distribution of loads at each suction cup while grasping objects. To solve for this load distribution, we find minimum spring potential energy configurations through a simple quadratic program. This results in a computationally efficient analytical solution that can be integrated to formulate grasp failure constraints in time-optimal trajectory planning. Finally, we present experimental results to validate the efficiency and accuracy of the proposed model.

On the Performance of Jerk-Constrained Time-Optimal Trajectory Planning for Industrial Manipulators

Jerk-constrained trajectories offer a wide range of advantages that collectively improve the performance of robotic systems, including increased energy efficiency, durability, and safety. In this paper, we present a novel approach to jerk-constrained time-optimal trajectory planning (TOTP), which follows a specified path while satisfying up to third-order constraints to ensure safety and smooth motion. One significant challenge in jerk-constrained TOTP is a non-convex formulation arising from the inclusion of third-order constraints. Approximating inequality constraints can be particularly challenging because the resulting solutions may violate the actual constraints. We address this problem by leveraging convexity within the proposed formulation to form conservative inequality constraints. We then obtain the desired trajectories by solving an $\boldsymbol n$-dimensional Sequential Linear Program (SLP) iteratively until convergence. Lastly, we evaluate in a real robot the performance of trajectories generated with and without jerk limits in terms of peak power, torque efficiency, and tracking capability.

Real-Time Model Predictive Control for Industrial Manipulators with Singularity-Tolerant Hierarchical Task Control

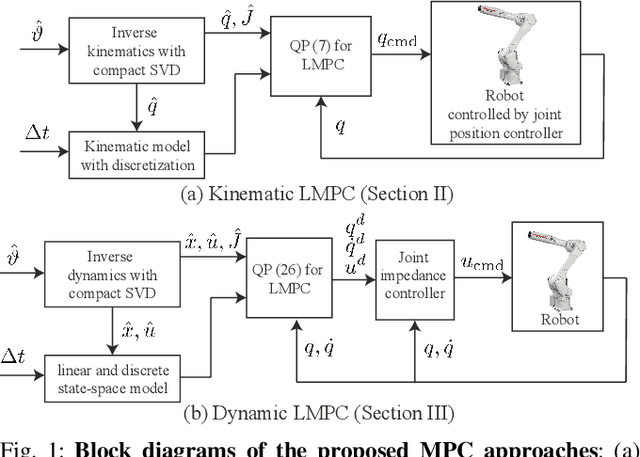
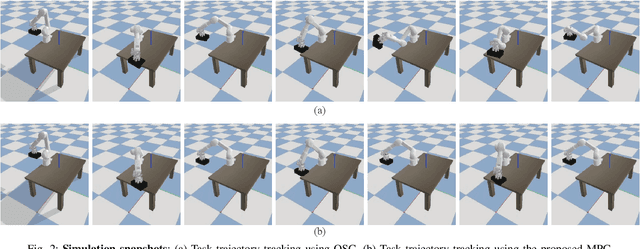
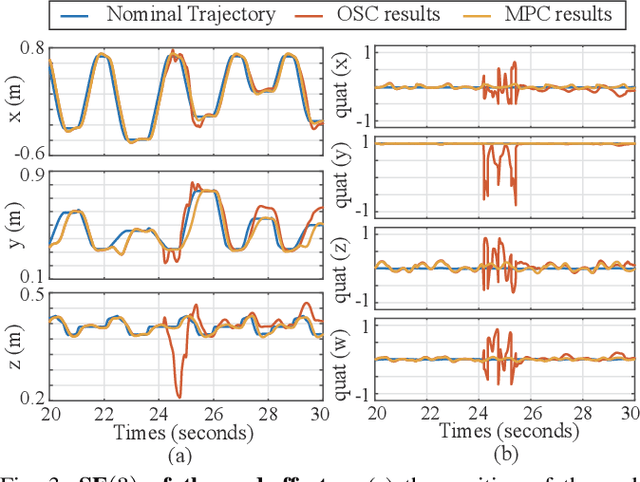
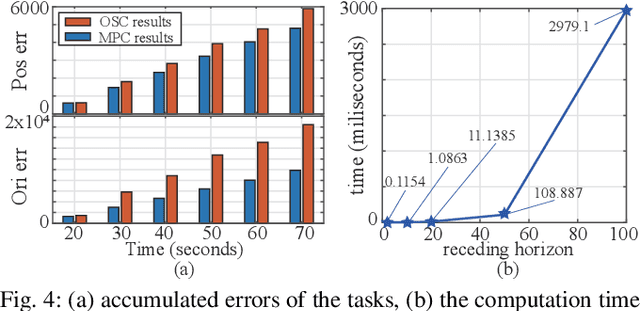
This paper proposes a real-time model predictive control (MPC) scheme to execute multiple tasks using robots over a finite-time horizon. In industrial robotic applications, we must carefully consider multiple constraints for avoiding joint position, velocity, and torque limits. In addition, singularity-free and smooth motions require executing tasks continuously and safely. Instead of formulating nonlinear MPC problems, we devise linear MPC problems using kinematic and dynamic models linearized along nominal trajectories produced by hierarchical controllers. These linear MPC problems are solvable via the use of Quadratic Programming; therefore, we significantly reduce the computation time of the proposed MPC framework so the resulting update frequency is higher than 1 kHz. Our proposed MPC framework is more efficient in reducing task tracking errors than a baseline based on operational space control (OSC). We validate our approach in numerical simulations and in real experiments using an industrial manipulator. More specifically, we deploy our method in two practical scenarios for robotic logistics: 1) controlling a robot carrying heavy payloads while accounting for torque limits, and 2) controlling the end-effector while avoiding singularities.