Grasp Failure Constraints for Fast and Reliable Pick-and-Place Using Multi-Suction-Cup Grippers

Multi-suction-cup grippers are frequently employed to perform pick-and-place robotic tasks, especially in industrial settings where grasping a wide range of light to heavy objects in limited amounts of time is a common requirement. However, most existing works focus on using one or two suction cups to grasp only irregularly shaped but light objects. There is a lack of research on robust manipulation of heavy objects using larger arrays of suction cups, which introduces challenges in modeling and predicting grasp failure. This paper presents a general approach to modeling grasp strength in multi-suction-cup grippers, introducing new constraints usable for trajectory planning and optimization to achieve fast and reliable pick-and-place maneuvers. The primary modeling challenge is the accurate prediction of the distribution of loads at each suction cup while grasping objects. To solve for this load distribution, we find minimum spring potential energy configurations through a simple quadratic program. This results in a computationally efficient analytical solution that can be integrated to formulate grasp failure constraints in time-optimal trajectory planning. Finally, we present experimental results to validate the efficiency and accuracy of the proposed model.

On the Performance of Jerk-Constrained Time-Optimal Trajectory Planning for Industrial Manipulators

Jerk-constrained trajectories offer a wide range of advantages that collectively improve the performance of robotic systems, including increased energy efficiency, durability, and safety. In this paper, we present a novel approach to jerk-constrained time-optimal trajectory planning (TOTP), which follows a specified path while satisfying up to third-order constraints to ensure safety and smooth motion. One significant challenge in jerk-constrained TOTP is a non-convex formulation arising from the inclusion of third-order constraints. Approximating inequality constraints can be particularly challenging because the resulting solutions may violate the actual constraints. We address this problem by leveraging convexity within the proposed formulation to form conservative inequality constraints. We then obtain the desired trajectories by solving an $\boldsymbol n$-dimensional Sequential Linear Program (SLP) iteratively until convergence. Lastly, we evaluate in a real robot the performance of trajectories generated with and without jerk limits in terms of peak power, torque efficiency, and tracking capability.

Sample Efficient Dynamics Learning for Symmetrical Legged Robots:Leveraging Physics Invariance and Geometric Symmetries

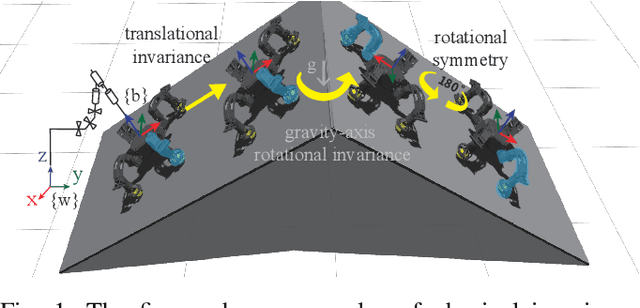
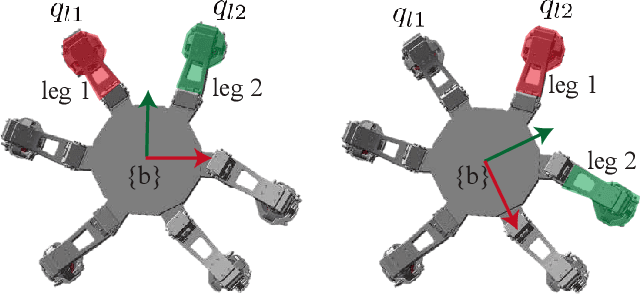
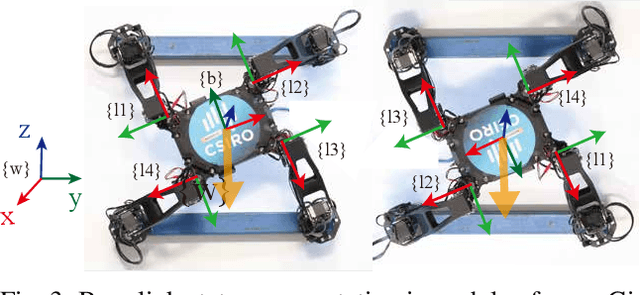
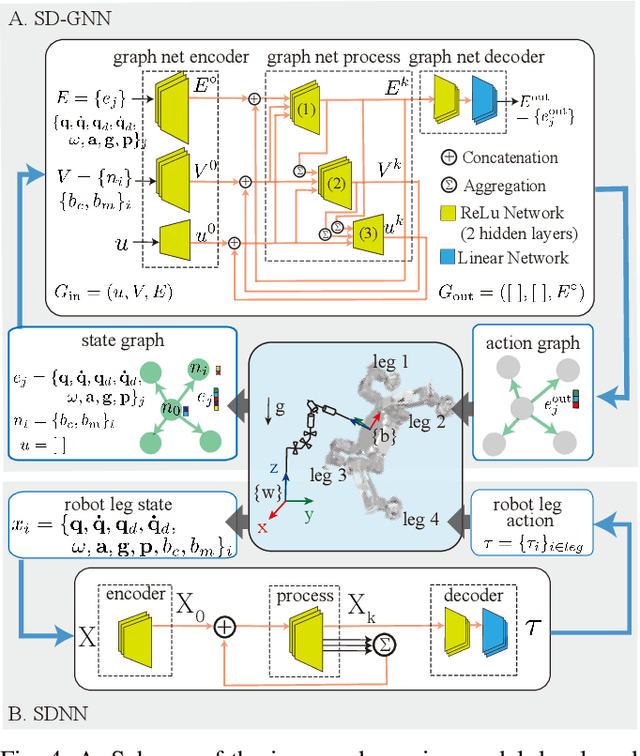
Model generalization of the underlying dynamics is critical for achieving data efficiency when learning for robot control. This paper proposes a novel approach for learning dynamics leveraging the symmetry in the underlying robotic system, which allows for robust extrapolation from fewer samples. Existing frameworks that represent all data in vector space fail to consider the structured information of the robot, such as leg symmetry, rotational symmetry, and physics invariance. As a result, these schemes require vast amounts of training data to learn the system's redundant elements because they are learned independently. Instead, we propose considering the geometric prior by representing the system in symmetrical object groups and designing neural network architecture to assess invariance and equivariance between the objects. Finally, we demonstrate the effectiveness of our approach by comparing the generalization to unseen data of the proposed model and the existing models. We also implement a controller of a climbing robot based on learned inverse dynamics models. The results show that our method generates accurate control inputs that help the robot reach the desired state while requiring less training data than existing methods.