Sample Efficient Dynamics Learning for Symmetrical Legged Robots:Leveraging Physics Invariance and Geometric Symmetries
Paper and Code
Oct 13, 2022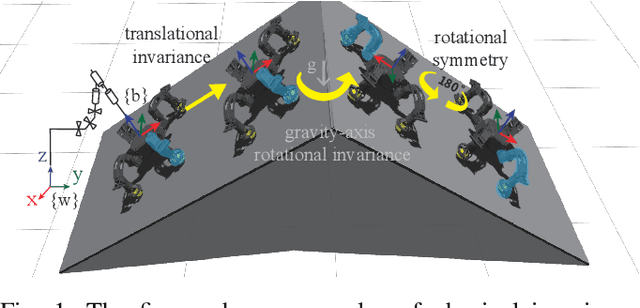
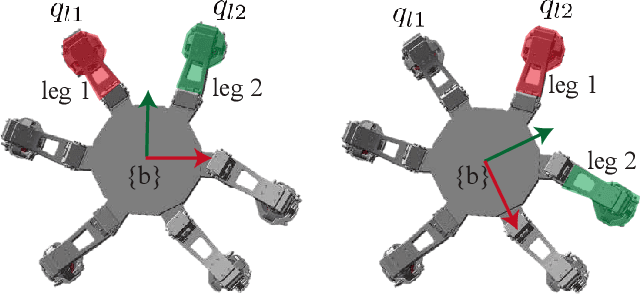
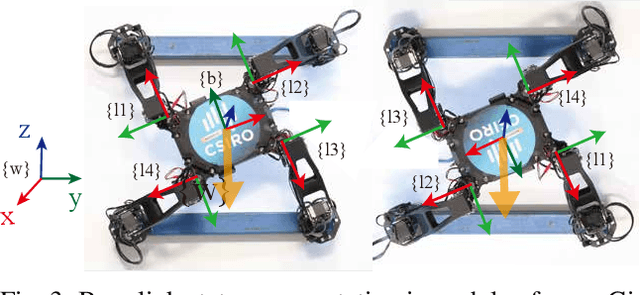
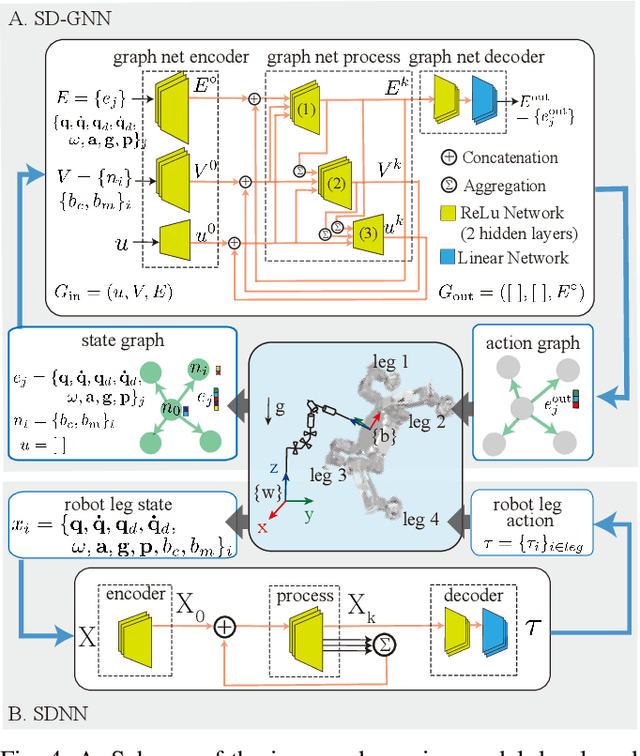
Model generalization of the underlying dynamics is critical for achieving data efficiency when learning for robot control. This paper proposes a novel approach for learning dynamics leveraging the symmetry in the underlying robotic system, which allows for robust extrapolation from fewer samples. Existing frameworks that represent all data in vector space fail to consider the structured information of the robot, such as leg symmetry, rotational symmetry, and physics invariance. As a result, these schemes require vast amounts of training data to learn the system's redundant elements because they are learned independently. Instead, we propose considering the geometric prior by representing the system in symmetrical object groups and designing neural network architecture to assess invariance and equivariance between the objects. Finally, we demonstrate the effectiveness of our approach by comparing the generalization to unseen data of the proposed model and the existing models. We also implement a controller of a climbing robot based on learned inverse dynamics models. The results show that our method generates accurate control inputs that help the robot reach the desired state while requiring less training data than existing methods.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge