SoGraB: A Visual Method for Soft Grasping Benchmarking and Evaluation

Recent years have seen soft robotic grippers gain increasing attention due to their ability to robustly grasp soft and fragile objects. However, a commonly available standardised evaluation protocol has not yet been developed to assess the performance of varying soft robotic gripper designs. This work introduces a novel protocol, the Soft Grasping Benchmarking and Evaluation (SoGraB) method, to evaluate grasping quality, which quantifies object deformation by using the Density-Aware Chamfer Distance (DCD) between point clouds of soft objects before and after grasping. We validated our protocol in extensive experiments, which involved ranking three Fin-Ray gripper designs with a subset of the EGAD object dataset. The protocol appropriately ranked grippers based on object deformation information, validating the method's ability to select soft grippers for complex grasping tasks and benchmark them for comparison against future designs.

DexGrip: Multi-modal Soft Gripper with Dexterous Grasping and In-hand Manipulation Capacity

The ability of robotic grippers to not only grasp but also re-position and re-orient objects in-hand is crucial for achieving versatile, general-purpose manipulation. While recent advances in soft robotic grasping has greatly improved grasp quality and stability, their manipulation capabilities remain under-explored. This paper presents the DexGrip, a multi-modal soft robotic gripper for in-hand grasping, re-orientation and manipulation. DexGrip features a 3 Degrees of Freedom (DoFs) active suction palm and 3 active (rotating) grasping surfaces, enabling soft, stable, and dexterous grasping and manipulation without ever needing to re-grasp an object. Uniquely, these features enable complete 360 degree rotation in all three principal axes. We experimentally demonstrate these capabilities across a diverse set of objects and tasks. DexGrip successfully grasped, re-positioned, and re-oriented objects with widely varying stiffnesses, sizes, weights, and surface textures; and effectively manipulated objects that presented significant challenges for existing robotic grippers.

Learning to Simulate Tree-Branch Dynamics for Manipulation

We propose to use a simulation driven inverse inference approach to model the joint dynamics of tree branches under manipulation. Learning branch dynamics and gaining the ability to manipulate deformable vegetation can help with occlusion-prone tasks, such as fruit picking in dense foliage, as well as moving overhanging vines and branches for navigation in dense vegetation. The underlying deformable tree geometry is encapsulated as coarse spring abstractions executed on parallel, non-differentiable simulators. The implicit statistical model defined by the simulator, reference trajectories obtained by actively probing the ground truth, and the Bayesian formalism, together guide the spring parameter posterior density estimation. Our non-parametric inference algorithm, based on Stein Variational Gradient Descent, incorporates biologically motivated assumptions into the inference process as neural network driven learnt joint priors; moreover, it leverages the finite difference scheme for gradient approximations. Real and simulated experiments confirm that our model can predict deformation trajectories, quantify the estimation uncertainty, and it can perform better when base-lined against other inference algorithms, particularly from the Monte Carlo family. The model displays strong robustness properties in the presence of heteroscedastic sensor noise; furthermore, it can generalise to unseen grasp locations.

Sample Efficient Dynamics Learning for Symmetrical Legged Robots:Leveraging Physics Invariance and Geometric Symmetries

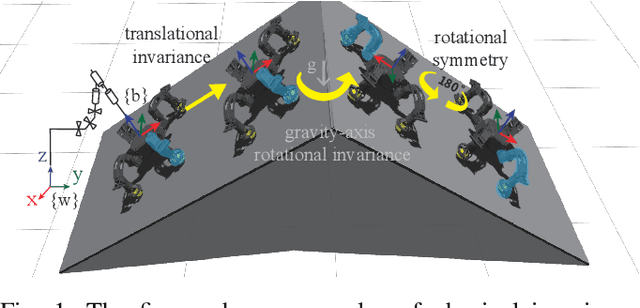
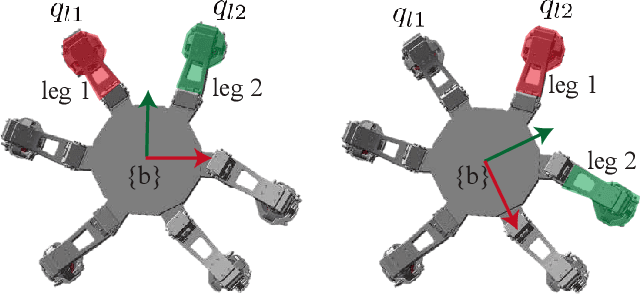
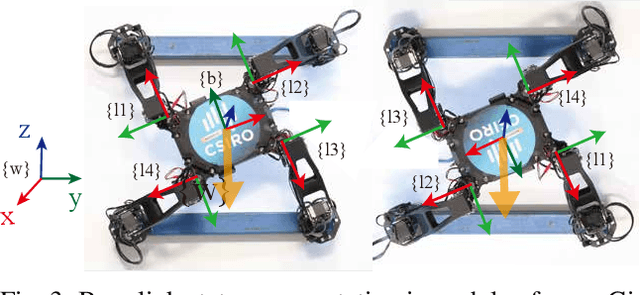
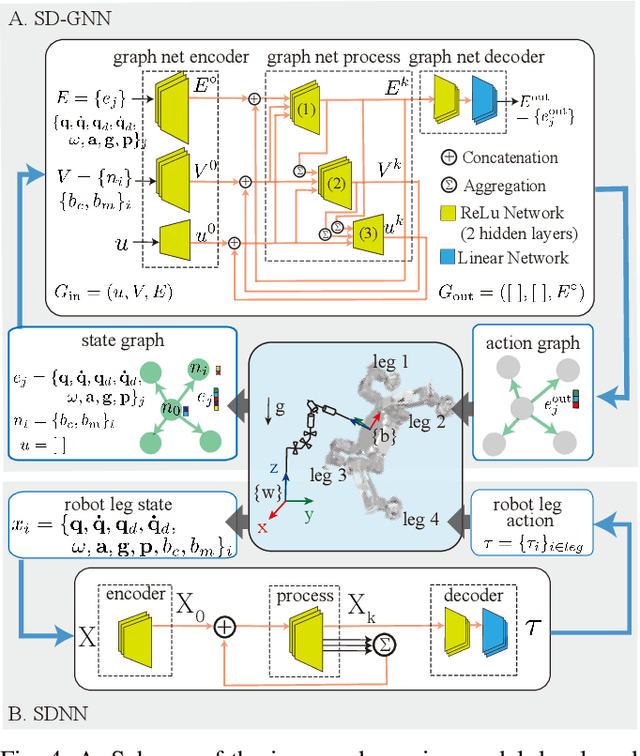
Model generalization of the underlying dynamics is critical for achieving data efficiency when learning for robot control. This paper proposes a novel approach for learning dynamics leveraging the symmetry in the underlying robotic system, which allows for robust extrapolation from fewer samples. Existing frameworks that represent all data in vector space fail to consider the structured information of the robot, such as leg symmetry, rotational symmetry, and physics invariance. As a result, these schemes require vast amounts of training data to learn the system's redundant elements because they are learned independently. Instead, we propose considering the geometric prior by representing the system in symmetrical object groups and designing neural network architecture to assess invariance and equivariance between the objects. Finally, we demonstrate the effectiveness of our approach by comparing the generalization to unseen data of the proposed model and the existing models. We also implement a controller of a climbing robot based on learned inverse dynamics models. The results show that our method generates accurate control inputs that help the robot reach the desired state while requiring less training data than existing methods.

Walking Posture Adaptation for Legged Robot Navigation in Confined Spaces

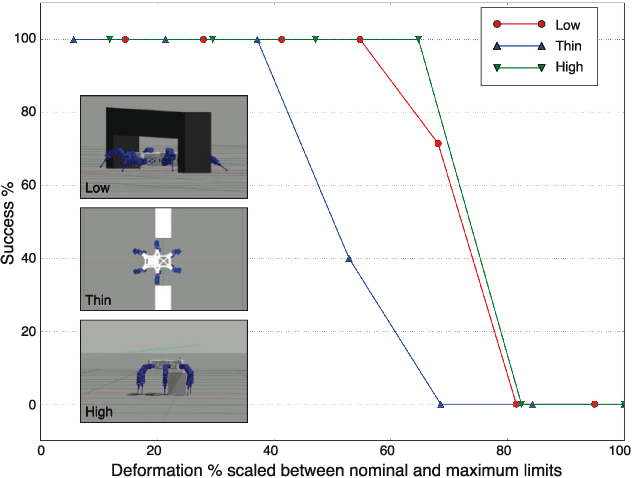
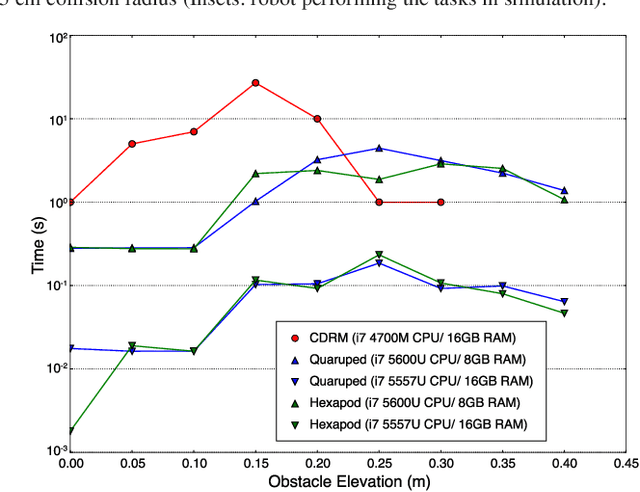
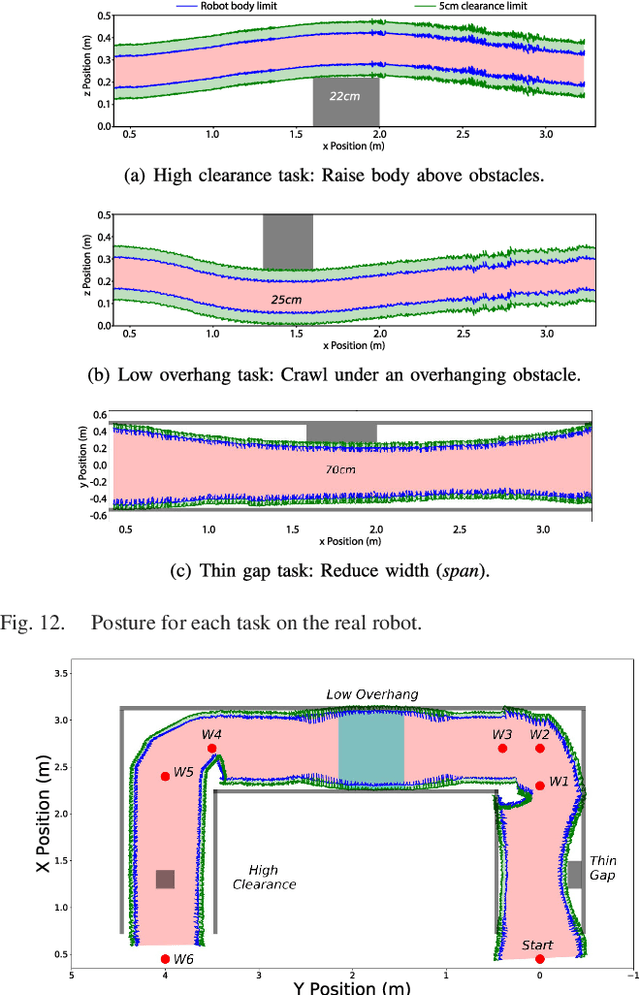
Legged robots have the ability to adapt their walking posture to navigate confined spaces due to their high degrees of freedom. However, this has not been exploited in most common multilegged platforms. This paper presents a deformable bounding box abstraction of the robot model, with accompanying mapping and planning strategies, that enable a legged robot to autonomously change its body shape to navigate confined spaces. The mapping is achieved using robot-centric multi-elevation maps generated with distance sensors carried by the robot. The path planning is based on the trajectory optimisation algorithm CHOMP which creates smooth trajectories while avoiding obstacles. The proposed method has been tested in simulation and implemented on the hexapod robot Weaver, which is 33cm tall and 82cm wide when walking normally. We demonstrate navigating under 25cm overhanging obstacles, through 70cm wide gaps and over 22cm high obstacles in both artificial testing spaces and realistic environments, including a subterranean mining tunnel.

Building Models for Biopathway Dynamics Using Intrinsic Dimensionality Analysis

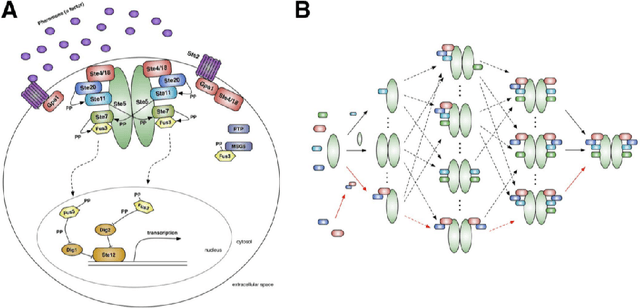
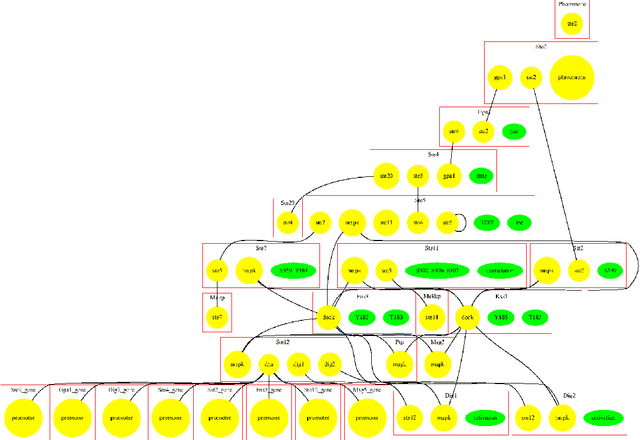
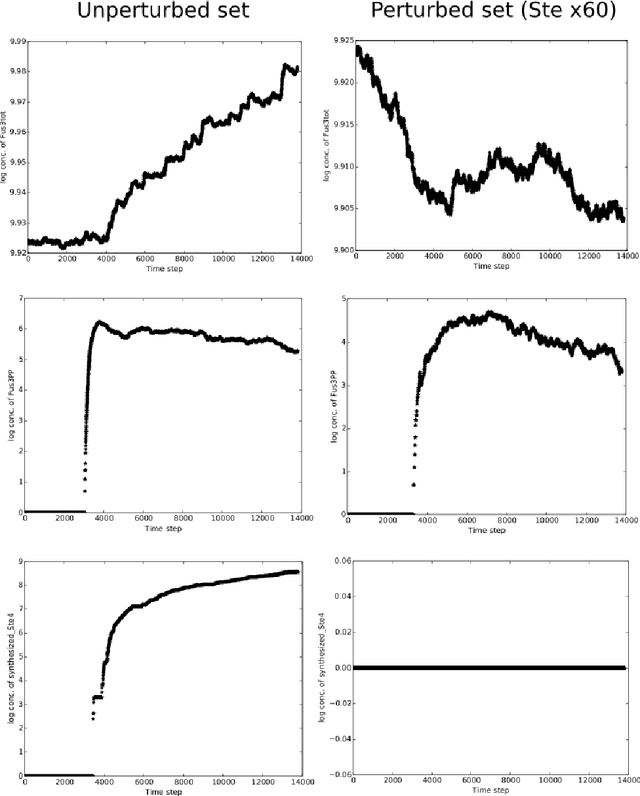
An important task for many if not all the scientific domains is efficient knowledge integration, testing and codification. It is often solved with model construction in a controllable computational environment. In spite of that, the throughput of in-silico simulation-based observations become similarly intractable for thorough analysis. This is especially the case in molecular biology, which served as a subject for this study. In this project, we aimed to test some approaches developed to deal with the curse of dimensionality. Among these we found dimension reduction techniques especially appealing. They can be used to identify irrelevant variability and help to understand critical processes underlying high-dimensional datasets. Additionally, we subjected our data sets to nonlinear time series analysis, as those are well established methods for results comparison. To investigate the usefulness of dimension reduction methods, we decided to base our study on a concrete sample set. The example was taken from the domain of systems biology concerning dynamic evolution of sub-cellular signaling. Particularly, the dataset relates to the yeast pheromone pathway and is studied in-silico with a stochastic model. The model reconstructs signal propagation stimulated by a mating pheromone. In the paper, we elaborate on the reason of multidimensional analysis problem in the context of molecular signaling, and next, we introduce the model of choice, simulation details and obtained time series dynamics. A description of used methods followed by a discussion of results and their biological interpretation finalize the paper.