Taming High-Dimensional Dynamics: Learning Optimal Projections onto Spectral Submanifolds

High-dimensional nonlinear systems pose considerable challenges for modeling and control across many domains, from fluid mechanics to advanced robotics. Such systems are typically approximated with reduced order models, which often rely on orthogonal projections, a simplification that may lead to large prediction errors. In this work, we derive optimality of fiber-aligned projections onto spectral submanifolds, preserving the nonlinear geometric structure and minimizing long-term prediction error. We propose a computationally tractable procedure to approximate these projections from data, and show how the effect of control can be incorporated. For a 180-dimensional robotic system, we demonstrate that our reduced-order models outperform previous state-of-the-art approaches by up to fivefold in trajectory tracking accuracy under model predictive control.

Data-Driven Soft Robot Control via Adiabatic Spectral Submanifolds

The mechanical complexity of soft robots creates significant challenges for their model-based control. Specifically, linear data-driven models have struggled to control soft robots on complex, spatially extended paths that explore regions with significant nonlinear behavior. To account for these nonlinearities, we develop here a model-predictive control strategy based on the recent theory of adiabatic spectral submanifolds (aSSMs). This theory is applicable because the internal vibrations of heavily overdamped robots decay at a speed that is much faster than the desired speed of the robot along its intended path. In that case, low-dimensional attracting invariant manifolds (aSSMs) emanate from the path and carry the dominant dynamics of the robot. Aided by this recent theory, we devise an aSSM-based model-predictive control scheme purely from data. We demonstrate the effectiveness of this data-driven model on various dynamic trajectory tracking tasks on a high-fidelity and high-dimensional finite-element model of a soft trunk robot. Notably, we find that four- or five-dimensional aSSM-reduced models outperform the tracking performance of other data-driven modeling methods by a factor up to 10 across all closed-loop control tasks.

Robust Nonlinear Reduced-Order Model Predictive Control

Real-world systems are often characterized by high-dimensional nonlinear dynamics, making them challenging to control in real time. While reduced-order models (ROMs) are frequently employed in model-based control schemes, dimensionality reduction introduces model uncertainty which can potentially compromise the stability and safety of the original high-dimensional system. In this work, we propose a novel reduced-order model predictive control (ROMPC) scheme to solve constrained optimal control problems for nonlinear, high-dimensional systems. To address the challenges of using ROMs in predictive control schemes, we derive an error bounding system that dynamically accounts for model reduction error. Using these bounds, we design a robust MPC scheme that ensures robust constraint satisfaction, recursive feasibility, and asymptotic stability. We demonstrate the effectiveness of our proposed method in simulations on a high-dimensional soft robot with nearly 10,000 states.

Data-Driven Spectral Submanifold Reduction for Nonlinear Optimal Control of High-Dimensional Robots

Modeling and control of high-dimensional, nonlinear robotic systems remains a challenging task. While various model- and learning-based approaches have been proposed to address these challenges, they broadly lack generalizability to different control tasks and rarely preserve the structure of the dynamics. In this work, we propose a new, data-driven approach for extracting low-dimensional models from data using Spectral Submanifold Reduction (SSMR). In contrast to other data-driven methods which fit dynamical models to training trajectories, we identify the dynamics on generic, low-dimensional attractors embedded in the full phase space of the robotic system. This allows us to obtain computationally-tractable models for control which preserve the system's dominant dynamics and better track trajectories radically different from the training data. We demonstrate the superior performance and generalizability of SSMR in dynamic trajectory tracking tasks vis-a-vis the state of the art, including Koopman operator-based approaches.

Using Spectral Submanifolds for Nonlinear Periodic Control

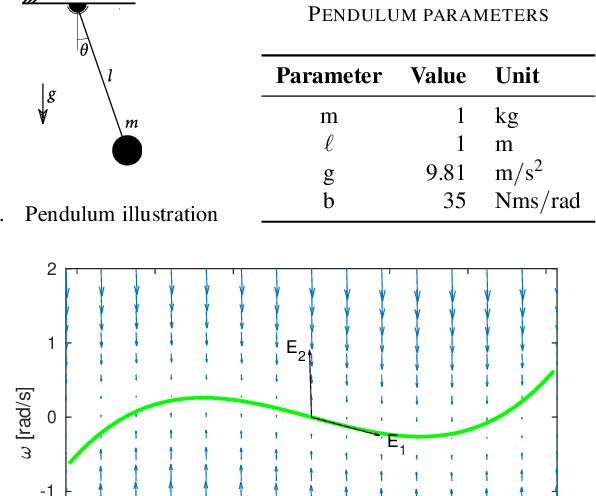
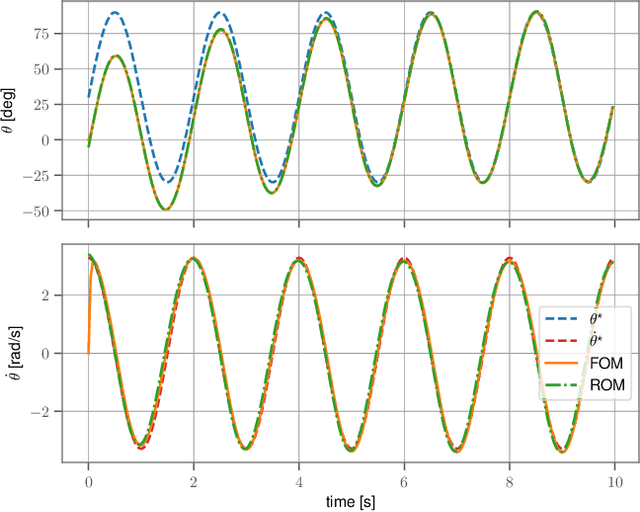
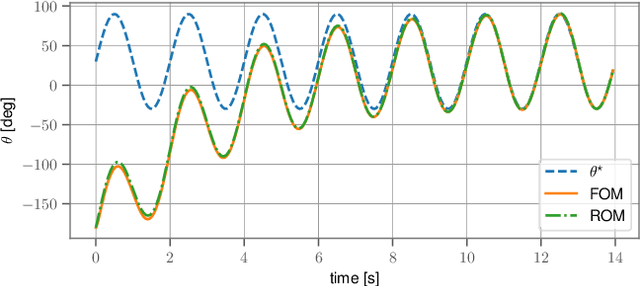
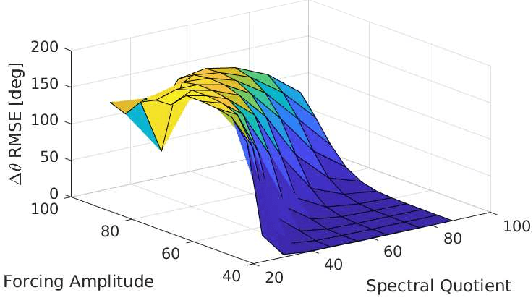
Very high dimensional nonlinear systems arise in many engineering problems due to semi-discretization of the governing partial differential equations, e.g. through finite element methods. The complexity of these systems present computational challenges for direct application to automatic control. While model reduction has seen ubiquitous applications in control, the use of nonlinear model reduction methods in this setting remains difficult. The problem lies in preserving the structure of the nonlinear dynamics in the reduced order model for high-fidelity control. In this work, we leverage recent advances in Spectral Submanifold (SSM) theory to enable model reduction under well-defined assumptions for the purpose of efficiently synthesizing feedback controllers.

Data-Driven Modeling and Prediction of Non-Linearizable Dynamics via Spectral Submanifolds

We develop a methodology to construct low-dimensional predictive models from data sets representing essentially nonlinear (or non-linearizable) dynamical systems with a hyperbolic linear part that are subject to external forcing with finitely many frequencies. Our data-driven, sparse, nonlinear models are obtained as extended normal forms of the reduced dynamics on low-dimensional, attracting spectral submanifolds (SSMs) of the dynamical system. We illustrate the power of data-driven SSM reduction on high-dimensional numerical data sets and experimental measurements involving beam oscillations, vortex shedding and sloshing in a water tank. We find that SSM reduction trained on unforced data also predicts nonlinear response accurately under additional external forcing.

Data-driven Nonlinear Model Reduction to Spectral Submanifolds in Mechanical Systems

While data-driven model reduction techniques are well-established for linearizable mechanical systems, general approaches to reducing non-linearizable systems with multiple coexisting steady states have been unavailable. In this paper, we review such a data-driven nonlinear model reduction methodology based on spectral submanifolds (SSMs). As input, this approach takes observations of unforced nonlinear oscillations to construct normal forms of the dynamics reduced to very low dimensional invariant manifolds. These normal forms capture amplitude-dependent properties and are accurate enough to provide predictions for non-linearizable system response under the additions of external forcing. We illustrate these results on examples from structural vibrations, featuring both synthetic and experimental data.