RRT2.0 for Fast and Optimal Kinodynamic Sampling-Based Motion Planning

We present RRT2.0: a simple yet efficient tree-based planner for asymptotically-optimal motion planning with kinodynamic constraints. RRT2.0 uses forward propagation and does not rely on the availability of a two-point boundary-value solver. The latter is a limiting requirement for some kinodynamic planners that are asymptotically optimal. The proposed approach improves upon a technique by Hauser and Zhou (2016), who explore an augmented state space with an additional coordinate, which endows every point in space with its cost-to-come value. Importantly, our optimality proofs require a milder and easily-verifiable set of assumptions on the problem and system: Lipschitz-continuity of the cost function and the dynamics. In particular, we prove that for any system satisfying those assumptions, any trajectory having a piecewise-constant control function and positive clearance from obstacles can be approximated arbitrarily well by a trajectory found by RRT2.0. We provide experimental results demonstrating on a couple of robot models with kinodynamic constraints that RRT2.0 outperforms the existing alternatives in practice.

The Critical Radius in Sampling-based Motion Planning

We develop a new analysis of sampling-based motion planning in Euclidean space with uniform random sampling, which significantly improves upon the celebrated result of Karaman and Frazzoli (2011) and subsequent work. Particularly, we prove the existence of a critical connection radius proportional to ${\Theta(n^{-1/d})}$ for $n$ samples and ${d}$ dimensions: Below this value the planner is guaranteed to fail (similarly shown by the aforementioned work, ibid.). More importantly, for larger radius values the planner is asymptotically (near-)optimal. Furthermore, our analysis yields an explicit lower bound of ${1-O( n^{-1})}$ on the probability of success. A practical implication of our work is that asymptotic (near-)optimality is achieved when each sample is connected to only ${\Theta(1)}$ neighbors. This is in stark contrast to previous work which requires ${\Theta(\log n)}$ connections, that are induced by a radius of order ${\left(\frac{\log n}{n}\right)^{1/d}}$. Our analysis is not restricted to PRM and applies to a variety of PRM-based planners, including RRG, FMT* and BTT. Continuum percolation plays an important role in our proofs. Lastly, we develop similar theory for all the aforementioned planners when constructed with deterministic samples, which are then sparsified in a randomized fashion. We believe that this new model, and its analysis, is interesting in its own right.

Probabilistic completeness of RRT for geometric and kinodynamic planning with forward propagation

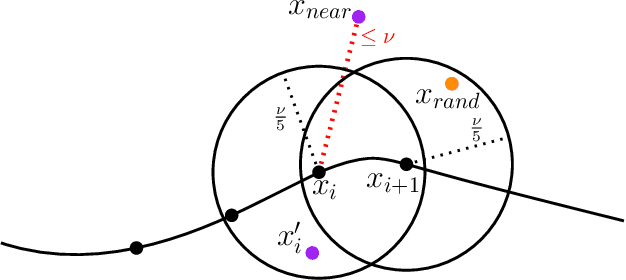
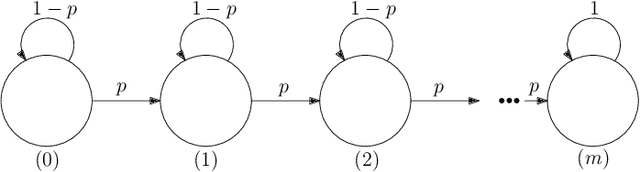
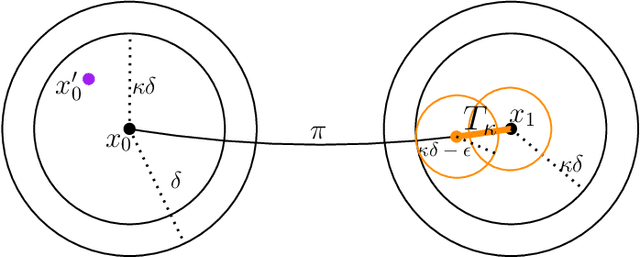
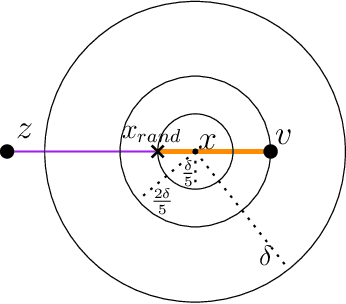
The Rapidly-exploring Random Tree (RRT) algorithm has been one of the most prevalent and popular motion-planning techniques for two decades now. Surprisingly, in spite of its centrality, there has been an active debate under which conditions RRT is probabilistically complete. We provide two new proofs of probabilistic completeness (PC) of RRT with a reduced set of assumptions. The first one for the purely geometric setting, where we only require that the solution path has a certain clearance from the obstacles. For the kinodynamic case with forward propagation of random controls and duration, we only consider in addition mild Lipschitz-continuity conditions. These proofs fill a gap in the study of RRT itself. They also lay sound foundations for a variety of more recent and alternative sampling-based methods, whose PC property relies on that of RRT.

Collision detection or nearest-neighbor search? On the computational bottleneck in sampling-based motion planning

The complexity of nearest-neighbor search dominates the asymptotic running time of many sampling-based motion-planning algorithms. However, collision detection is often considered to be the computational bottleneck in practice. Examining various asymptotically optimal planning algorithms, we characterize settings, which we call NN-sensitive, in which the practical computational role of nearest-neighbor search is far from being negligible, i.e., the portion of running time taken up by nearest-neighbor search is comparable, or sometimes even greater than the portion of time taken up by collision detection. This reinforces and substantiates the claim that motion-planning algorithms could significantly benefit from efficient and possibly specifically-tailored nearest-neighbor data structures. The asymptotic (near) optimality of these algorithms relies on a prescribed connection radius, defining a ball around a configuration $q$, such that $q$ needs to be connected to all other configurations in that ball. To facilitate our study, we show how to adapt this radius to non-Euclidean spaces, which are prevalent in motion planning. This technical result is of independent interest, as it enables to compare the radial-connection approach with the common alternative, namely, connecting each configuration to its $k$ nearest neighbors ($k$-NN). Indeed, as we demonstrate, there are scenarios where using the radial connection scheme, a solution path of a specific cost is produced ten-fold (and more) faster than with $k$-NN.

Efficient high-quality motion planning by fast all-pairs r-nearest-neighbors

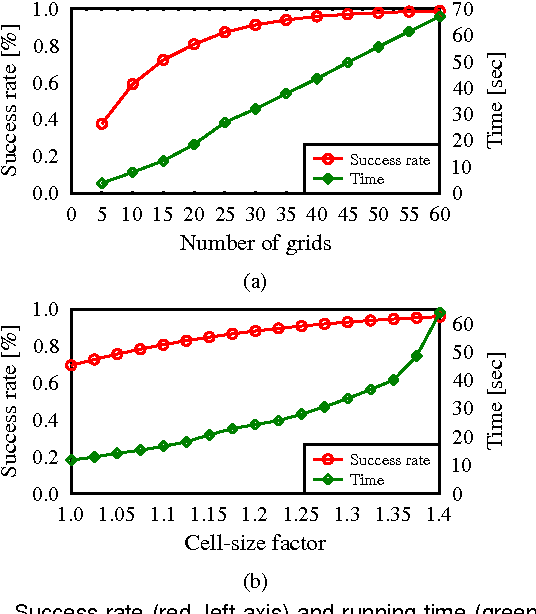
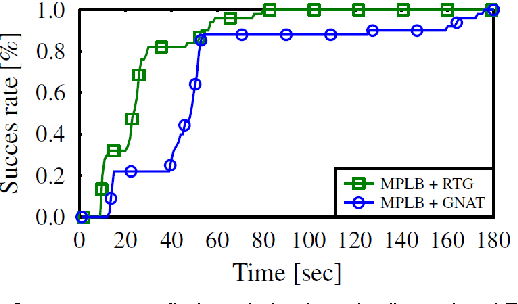
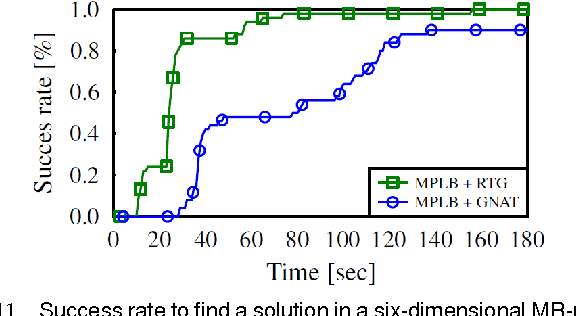
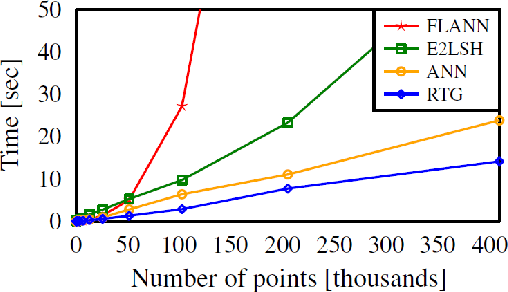
Sampling-based motion-planning algorithms typically rely on nearest-neighbor (NN) queries when constructing a roadmap. Recent results suggest that in various settings NN queries may be the computational bottleneck of such algorithms. Moreover, in several asymptotically-optimal algorithms these NN queries are of a specific form: Given a set of points and a radius r report all pairs of points whose distance is at most r. This calls for an application-specific NN data structure tailored to efficiently answering this type of queries. Randomly transformed grids (RTG) were recently proposed by Aiger et al. as a tool to answer such queries and have been shown to outperform common implementations of NN data structures in this context. In this work we employ RTG for sampling-based motion-planning algorithms and describe an efficient implementation of the approach. We show that for motion-planning, RTG allow for faster convergence to high-quality solutions when compared with existing NN data structures. Additionally, RTG enable significantly shorter construction times for batched-PRM variants; specifically, we demonstrate a speedup by a factor of two to three for some scenarios.