Probabilistic completeness of RRT for geometric and kinodynamic planning with forward propagation

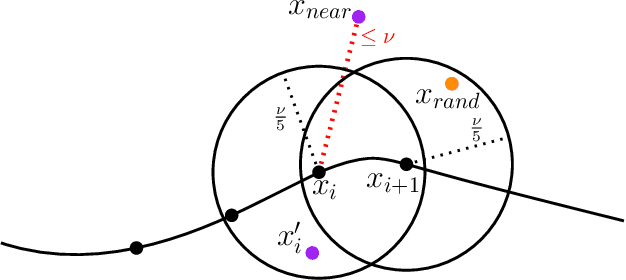
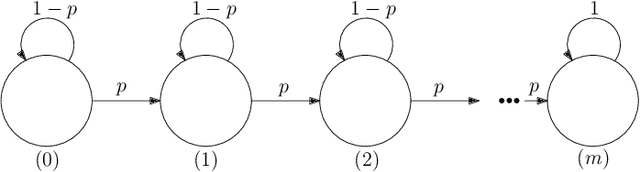
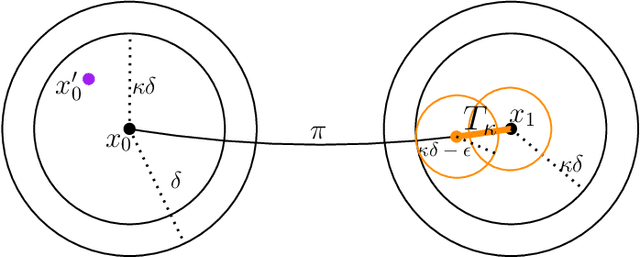
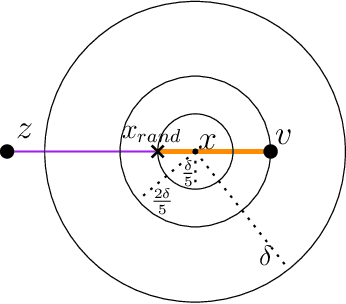
The Rapidly-exploring Random Tree (RRT) algorithm has been one of the most prevalent and popular motion-planning techniques for two decades now. Surprisingly, in spite of its centrality, there has been an active debate under which conditions RRT is probabilistically complete. We provide two new proofs of probabilistic completeness (PC) of RRT with a reduced set of assumptions. The first one for the purely geometric setting, where we only require that the solution path has a certain clearance from the obstacles. For the kinodynamic case with forward propagation of random controls and duration, we only consider in addition mild Lipschitz-continuity conditions. These proofs fill a gap in the study of RRT itself. They also lay sound foundations for a variety of more recent and alternative sampling-based methods, whose PC property relies on that of RRT.