Towards Learning Efficient Maneuver Sets for Kinodynamic Motion Planning

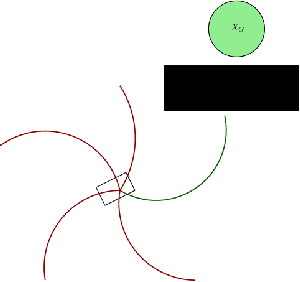
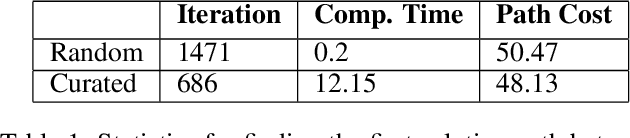
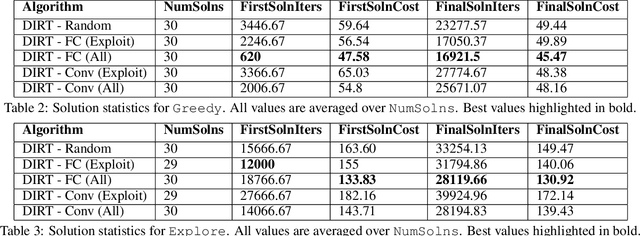
Planning for systems with dynamics is challenging as often there is no local planner available and the only primitive to explore the state space is forward propagation of controls. In this context, tree sampling-based planners have been developed, some of which achieve asymptotic optimality by propagating random controls during each iteration. While desirable for the analysis, random controls result in slow convergence to high quality trajectories in practice. This short position statement first argues that if a kinodynamic planner has access to local maneuvers that appropriately balance an exploitation-exploration trade-off, the planner's per iteration performance is significantly improved. Generating such maneuvers during planning can be achieved by curating a large sample of random controls. This is, however, computationally very expensive. If such maneuvers can be generated fast, the planner's performance will also improve as a function of computation time. Towards objective, this short position statement argues for the integration of modern machine learning frameworks with state-of-the-art, informed and asymptotically optimal kinodynamic planners. The proposed approach involves using using neural networks to infer local maneuvers for a robotic system with dynamics, which properly balance the above exploitation-exploration trade-off. In particular, a neural network architecture is proposed, which is trained to reflect the choices of an online curation process, given local obstacle and heuristic information. The planner uses these maneuvers to efficiently explore the underlying state space, while still maintaining desirable properties. Preliminary indications in simulated environments and systems are promising but also point to certain challenges that motivate further research in this direction.

Fast, Anytime Motion Planning for Prehensile Manipulation in Clutter

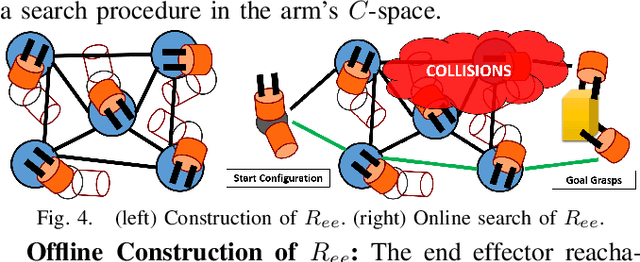
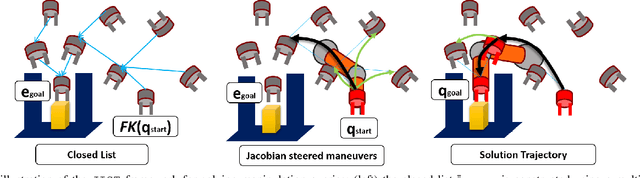
Many methods have been developed for planning the motion of robotic arms for picking and placing, ranging from local optimization to global search techniques, which are effective for sparsely placed objects. Dense clutter, however, still adversely affects the success rate, computation times, and quality of solutions in many real-world setups. The current work integrates tools from existing methodologies and proposes a framework that achieves high success ratio in clutter with anytime performance. The idea is to first explore the lower dimensional end effector's task space efficiently by ignoring the arm, and build a discrete approximation of a navigation function, which guides the end effector towards the set of available grasps or object placements. This is performed online, without prior knowledge of the scene. Then, an informed sampling-based planner for the entire arm uses Jacobian-based steering to reach promising end effector poses given the task space guidance. While informed, the method is also comprehensive and allows the exploration of alternative paths over time if the task space guidance does not lead to a solution. This paper evaluates the proposed method against alternatives in picking or placing tasks among varying amounts of clutter for a variety of robotic manipulators with different end-effectors. The results suggest that the method reliably provides higher quality solution paths quicker, with a higher success rate relative to alternatives.

Probabilistic completeness of RRT for geometric and kinodynamic planning with forward propagation

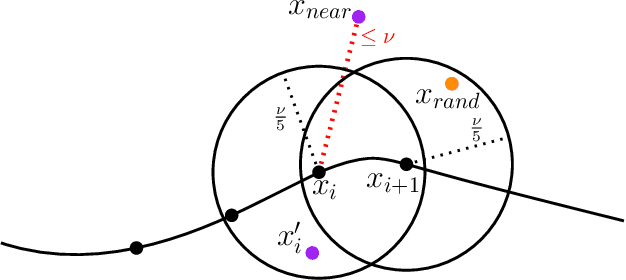
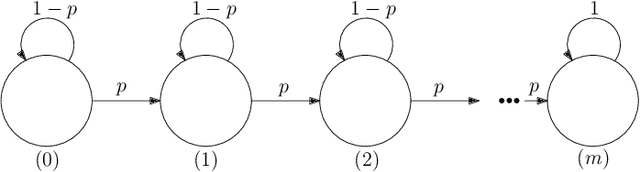
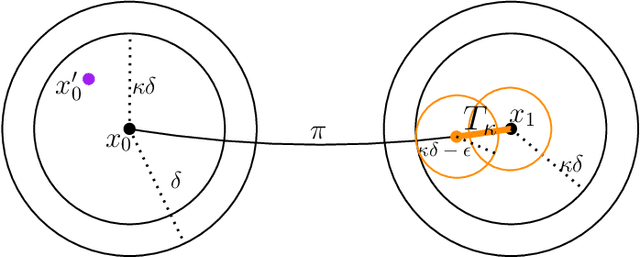
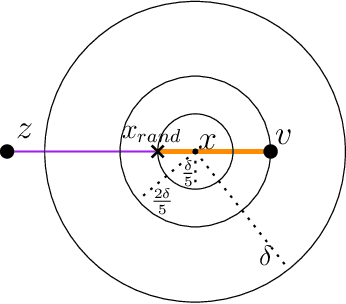
The Rapidly-exploring Random Tree (RRT) algorithm has been one of the most prevalent and popular motion-planning techniques for two decades now. Surprisingly, in spite of its centrality, there has been an active debate under which conditions RRT is probabilistically complete. We provide two new proofs of probabilistic completeness (PC) of RRT with a reduced set of assumptions. The first one for the purely geometric setting, where we only require that the solution path has a certain clearance from the obstacles. For the kinodynamic case with forward propagation of random controls and duration, we only consider in addition mild Lipschitz-continuity conditions. These proofs fill a gap in the study of RRT itself. They also lay sound foundations for a variety of more recent and alternative sampling-based methods, whose PC property relies on that of RRT.

Asymptotically Optimal Sampling-based Kinodynamic Planning

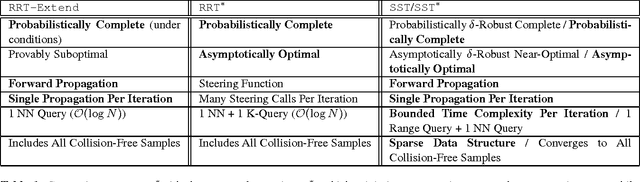
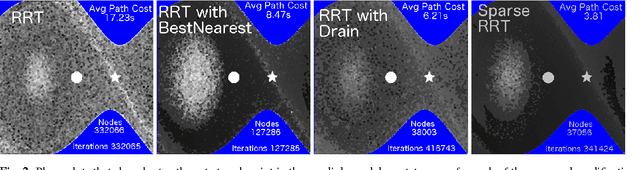
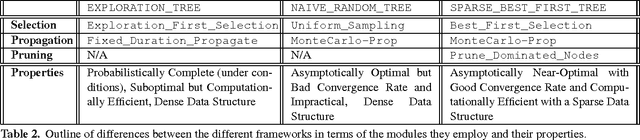
Sampling-based algorithms are viewed as practical solutions for high-dimensional motion planning. Recent progress has taken advantage of random geometric graph theory to show how asymptotic optimality can also be achieved with these methods. Achieving this desirable property for systems with dynamics requires solving a two-point boundary value problem (BVP) in the state space of the underlying dynamical system. It is difficult, however, if not impractical, to generate a BVP solver for a variety of important dynamical models of robots or physically simulated ones. Thus, an open challenge was whether it was even possible to achieve optimality guarantees when planning for systems without access to a BVP solver. This work resolves the above question and describes how to achieve asymptotic optimality for kinodynamic planning using incremental sampling-based planners by introducing a new rigorous framework. Two new methods, Stable Sparse-RRT (SST) and SST*, result from this analysis, which are asymptotically near-optimal and optimal, respectively. The techniques are shown to converge fast to high-quality paths, while they maintain only a sparse set of samples, which makes them computationally efficient. The good performance of the planners is confirmed by experimental results using dynamical systems benchmarks, as well as physically simulated robots.