Asymptotically Optimal Sampling-based Kinodynamic Planning
Paper and Code
Feb 05, 2016
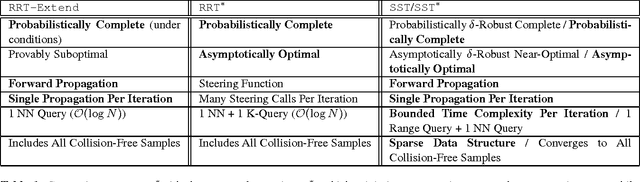
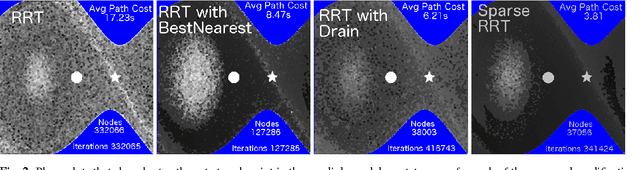
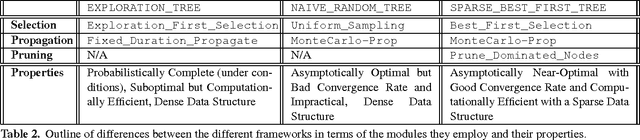
Sampling-based algorithms are viewed as practical solutions for high-dimensional motion planning. Recent progress has taken advantage of random geometric graph theory to show how asymptotic optimality can also be achieved with these methods. Achieving this desirable property for systems with dynamics requires solving a two-point boundary value problem (BVP) in the state space of the underlying dynamical system. It is difficult, however, if not impractical, to generate a BVP solver for a variety of important dynamical models of robots or physically simulated ones. Thus, an open challenge was whether it was even possible to achieve optimality guarantees when planning for systems without access to a BVP solver. This work resolves the above question and describes how to achieve asymptotic optimality for kinodynamic planning using incremental sampling-based planners by introducing a new rigorous framework. Two new methods, Stable Sparse-RRT (SST) and SST*, result from this analysis, which are asymptotically near-optimal and optimal, respectively. The techniques are shown to converge fast to high-quality paths, while they maintain only a sparse set of samples, which makes them computationally efficient. The good performance of the planners is confirmed by experimental results using dynamical systems benchmarks, as well as physically simulated robots.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge