HALO: Hazard-Aware Landing Optimization for Autonomous Systems

With autonomous aerial vehicles enacting safety-critical missions, such as the Mars Science Laboratory Curiosity rover's landing on Mars, the tasks of automatically identifying and reasoning about potentially hazardous landing sites is paramount. This paper presents a coupled perception-planning solution which addresses the hazard detection, optimal landing trajectory generation, and contingency planning challenges encountered when landing in uncertain environments. Specifically, we develop and combine two novel algorithms, Hazard-Aware Landing Site Selection (HALSS) and Adaptive Deferred-Decision Trajectory Optimization (Adaptive-DDTO), to address the perception and planning challenges, respectively. The HALSS framework processes point cloud information to identify feasible safe landing zones, while Adaptive-DDTO is a multi-target contingency planner that adaptively replans as new perception information is received. We demonstrate the efficacy of our approach using a simulated Martian environment and show that our coupled perception-planning method achieves greater landing success whilst being more fuel efficient compared to a nonadaptive DDTO approach.

Guided Policy Search using Sequential Convex Programming for Initialization of Trajectory Optimization Algorithms

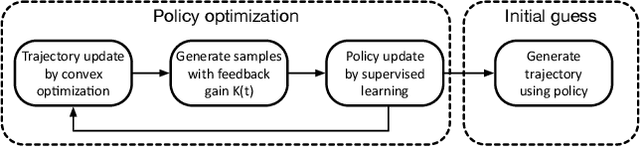
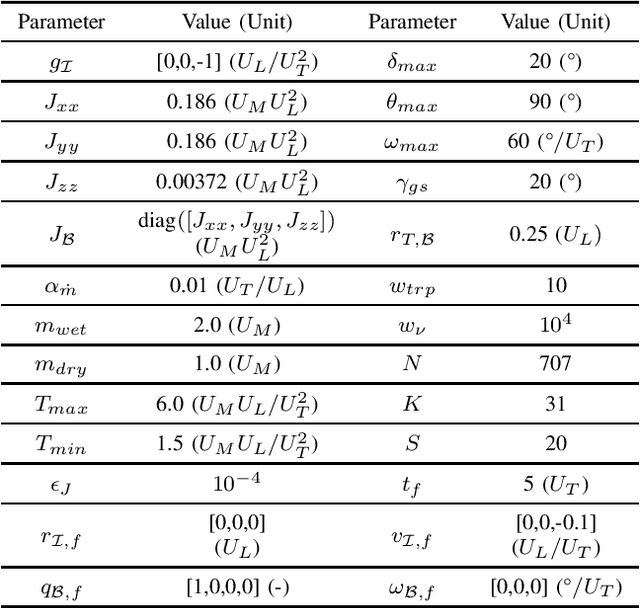
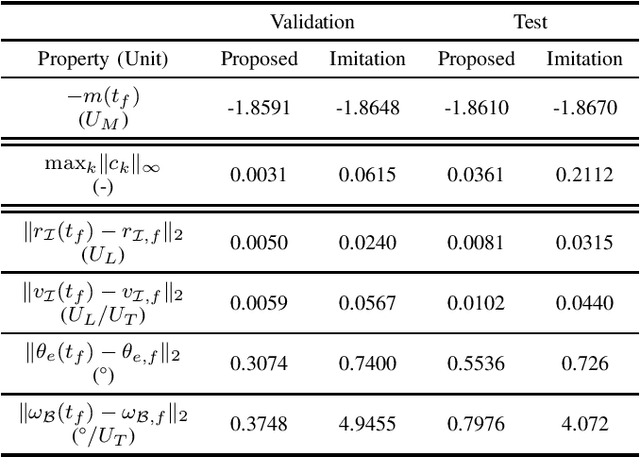
Nonlinear trajectory optimization algorithms have been developed to handle optimal control problems with nonlinear dynamics and nonconvex constraints in trajectory planning. The performance and computational efficiency of many trajectory optimization methods are sensitive to the initial guess, i.e., the trajectory guess needed by the recursive trajectory optimization algorithm. Motivated by this observation, we tackle the initialization problem for trajectory optimization via policy optimization. To optimize a policy, we propose a guided policy search method that has two key components: i) Trajectory update; ii) Policy update. The trajectory update involves offline solutions of a large number of trajectory optimization problems from different initial states via Sequential Convex Programming (SCP). Here we take a single SCP step to generate the trajectory iterate for each problem. In conjunction with these iterates, we also generate additional trajectories around each iterate via a feedback control law. Then all these trajectories are used by a stochastic gradient descent algorithm to update the neural network policy, i.e., the policy update step. As a result, the trained policy makes it possible to generate trajectory candidates that are close to the optimality and feasibility and that provide excellent initial guesses for the trajectory optimization methods. We validate the proposed method via a real-world 6-degree-of-freedom powered descent guidance problem for a reusable rocket.

Advances in Trajectory Optimization for Space Vehicle Control

Space mission design places a premium on cost and operational efficiency. The search for new science and life beyond Earth calls for spacecraft that can deliver scientific payloads to geologically rich yet hazardous landing sites. At the same time, the last four decades of optimization research have put a suite of powerful optimization tools at the fingertips of the controls engineer. As we enter the new decade, optimization theory, algorithms, and software tooling have reached a critical mass to start seeing serious application in space vehicle guidance and control systems. This survey paper provides a detailed overview of recent advances, successes, and promising directions for optimization-based space vehicle control. The considered applications include planetary landing, rendezvous and proximity operations, small body landing, constrained attitude reorientation, endo-atmospheric flight including ascent and reentry, and orbit transfer and injection. The primary focus is on the last ten years of progress, which have seen a veritable rise in the number of applications using three core technologies: lossless convexification, sequential convex programming, and model predictive control. The reader will come away with a well-rounded understanding of the state-of-the-art in each space vehicle control application, and will be well positioned to tackle important current open problems using convex optimization as a core technology.

Convex Optimization for Trajectory Generation

Reliable and efficient trajectory generation methods are a fundamental need for autonomous dynamical systems of tomorrow. The goal of this article is to provide a comprehensive tutorial of three major convex optimization-based trajectory generation methods: lossless convexification (LCvx), and two sequential convex programming algorithms known as SCvx and GuSTO. In this article, trajectory generation is the computation of a dynamically feasible state and control signal that satisfies a set of constraints while optimizing key mission objectives. The trajectory generation problem is almost always nonconvex, which typically means that it is not readily amenable to efficient and reliable solution onboard an autonomous vehicle. The three algorithms that we discuss use problem reformulation and a systematic algorithmic strategy to nonetheless solve nonconvex trajectory generation tasks through the use of a convex optimizer. The theoretical guarantees and computational speed offered by convex optimization have made the algorithms popular in both research and industry circles. To date, the list of applications includes rocket landing, spacecraft hypersonic reentry, spacecraft rendezvous and docking, aerial motion planning for fixed-wing and quadrotor vehicles, robot motion planning, and more. Among these applications are high-profile rocket flights conducted by organizations like NASA, Masten Space Systems, SpaceX, and Blue Origin. This article aims to give the reader the tools and understanding necessary to work with each algorithm, and to know what each method can and cannot do. A publicly available source code repository supports the provided numerical examples. By the end of the article, the reader should be ready to use the methods, to extend them, and to contribute to their many exciting modern applications.

Mixed Strategy for Constrained Stochastic Optimal Control

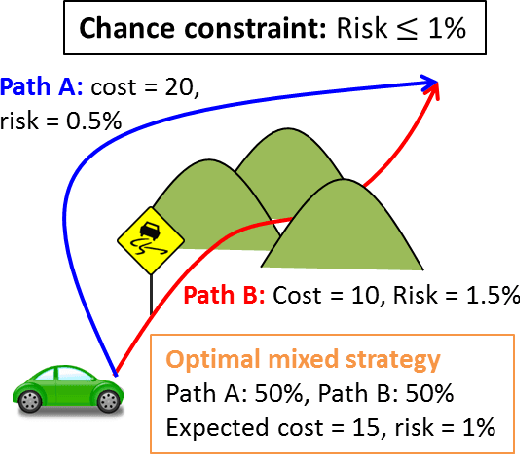
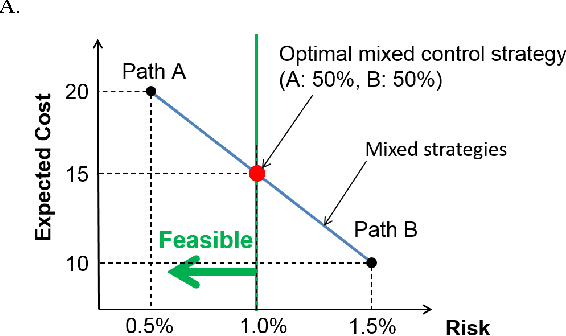
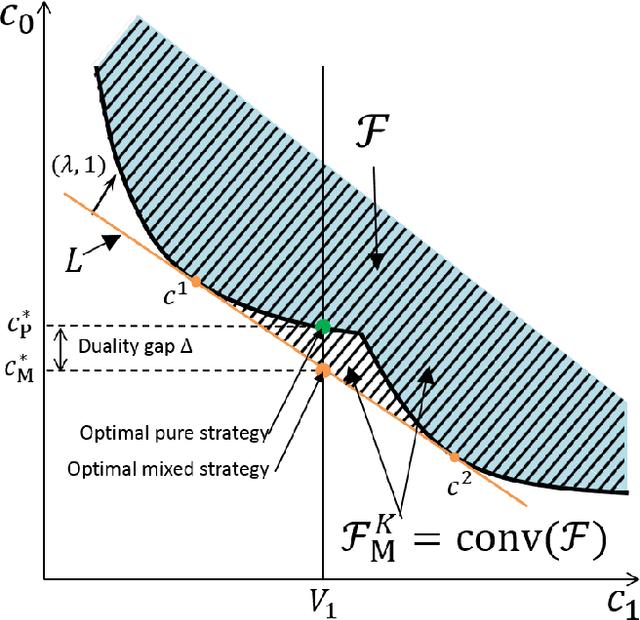
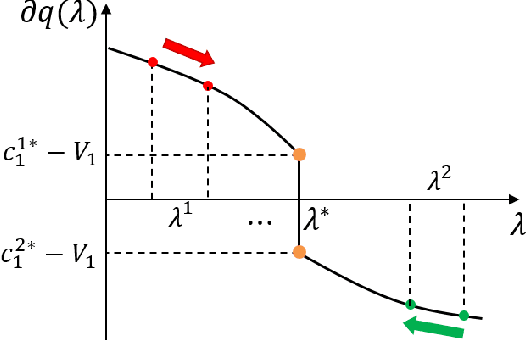
Choosing control inputs randomly can result in a reduced expected cost in optimal control problems with stochastic constraints, such as stochastic model predictive control (SMPC). We consider a controller with initial randomization, meaning that the controller randomly chooses from K+1 control sequences at the beginning (called K-randimization).It is known that, for a finite-state, finite-action Markov Decision Process (MDP) with K constraints, K-randimization is sufficient to achieve the minimum cost. We found that the same result holds for stochastic optimal control problems with continuous state and action spaces.Furthermore, we show the randomization of control input can result in reduced cost when the optimization problem is nonconvex, and the cost reduction is equal to the duality gap. We then provide the necessary and sufficient conditions for the optimality of a randomized solution, and develop an efficient solution method based on dual optimization. Furthermore, in a special case with K=1 such as a joint chance-constrained problem, the dual optimization can be solved even more efficiently by root finding. Finally, we test the theories and demonstrate the solution method on multiple practical problems ranging from path planning to the planning of entry, descent, and landing (EDL) for future Mars missions.