Mixed Strategy for Constrained Stochastic Optimal Control
Paper and Code
Jul 06, 2016
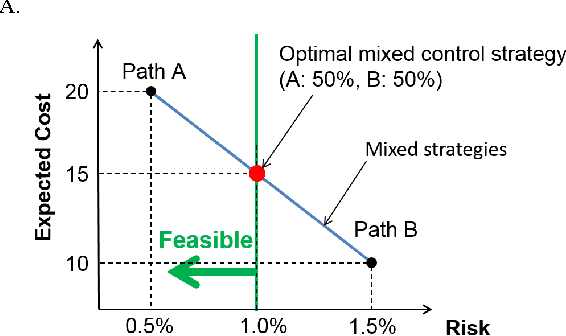
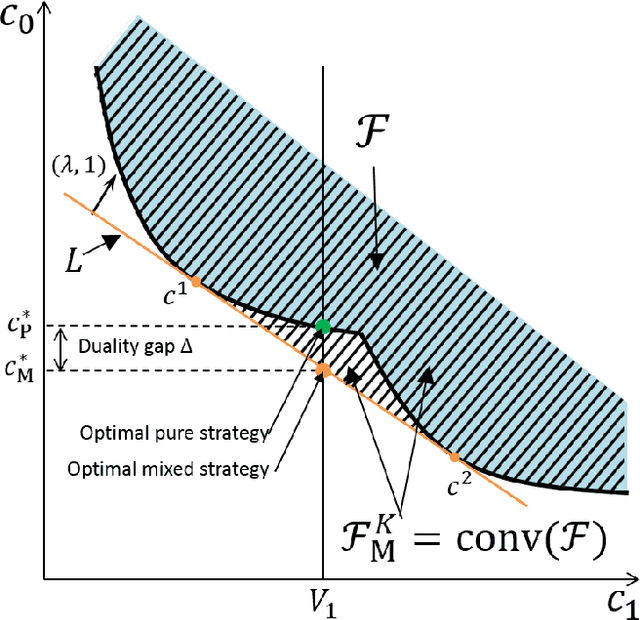
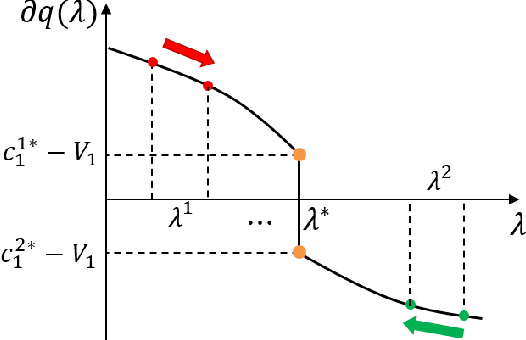
Choosing control inputs randomly can result in a reduced expected cost in optimal control problems with stochastic constraints, such as stochastic model predictive control (SMPC). We consider a controller with initial randomization, meaning that the controller randomly chooses from K+1 control sequences at the beginning (called K-randimization).It is known that, for a finite-state, finite-action Markov Decision Process (MDP) with K constraints, K-randimization is sufficient to achieve the minimum cost. We found that the same result holds for stochastic optimal control problems with continuous state and action spaces.Furthermore, we show the randomization of control input can result in reduced cost when the optimization problem is nonconvex, and the cost reduction is equal to the duality gap. We then provide the necessary and sufficient conditions for the optimality of a randomized solution, and develop an efficient solution method based on dual optimization. Furthermore, in a special case with K=1 such as a joint chance-constrained problem, the dual optimization can be solved even more efficiently by root finding. Finally, we test the theories and demonstrate the solution method on multiple practical problems ranging from path planning to the planning of entry, descent, and landing (EDL) for future Mars missions.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge