Linear Bandits with Memory: from Rotting to Rising

Nonstationary phenomena, such as satiation effects in recommendation, are a common feature of sequential decision-making problems. While these phenomena have been mostly studied in the framework of bandits with finitely many arms, in many practically relevant cases linear bandits provide a more effective modeling choice. In this work, we introduce a general framework for the study of nonstationary linear bandits, where current rewards are influenced by the learner's past actions in a fixed-size window. In particular, our model includes stationary linear bandits as a special case. After showing that the best sequence of actions is NP-hard to compute in our model, we focus on cyclic policies and prove a regret bound for a variant of the OFUL algorithm that balances approximation and estimation errors. Our theoretical findings are supported by experiments (which also include misspecified settings) where our algorithm is seen to perform well against natural baselines.

Break your Bandit Routine with LSD Rewards: a Last Switch Dependent Analysis of Satiation and Seasonality

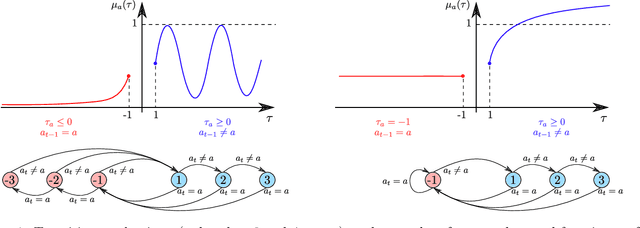
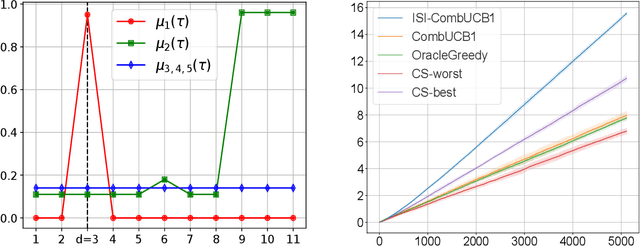
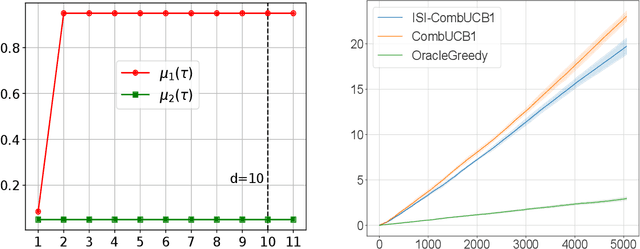
Motivated by the fact that humans like some level of unpredictability or novelty, and might therefore get quickly bored when interacting with a stationary policy, we introduce a novel non-stationary bandit problem, where the expected reward of an arm is fully determined by the time elapsed since the arm last took part in a switch of actions. Our model generalizes previous notions of delay-dependent rewards, and also relaxes most assumptions on the reward function. This enables the modeling of phenomena such as progressive satiation and periodic behaviours. Building upon the Combinatorial Semi-Bandits (CSB) framework, we design an algorithm and prove a bound on its regret with respect to the optimal non-stationary policy (which is NP-hard to compute). Similarly to previous works, our regret analysis is based on defining and solving an appropriate trade-off between approximation and estimation. Preliminary experiments confirm the superiority of our algorithm over both the oracle greedy approach and a vanilla CSB solver.