Dynamic Learning Rate for Deep Reinforcement Learning: A Bandit Approach

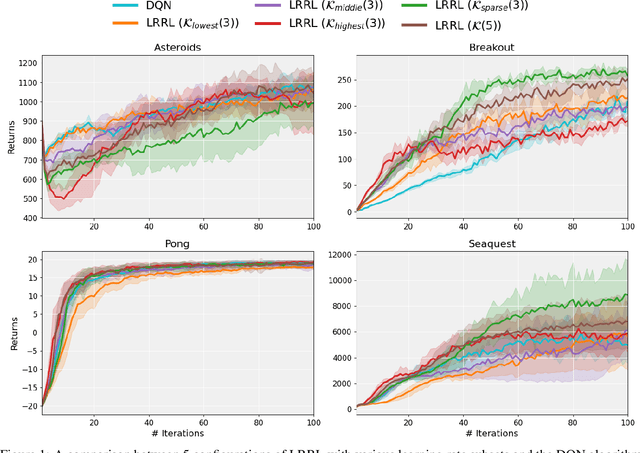
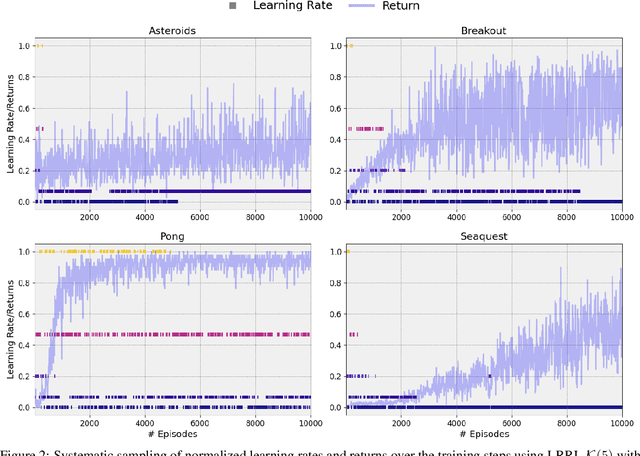
In Deep Reinforcement Learning models trained using gradient-based techniques, the choice of optimizer and its learning rate are crucial to achieving good performance: higher learning rates can prevent the model from learning effectively, while lower ones might slow convergence. Additionally, due to the non-stationarity of the objective function, the best-performing learning rate can change over the training steps. To adapt the learning rate, a standard technique consists of using decay schedulers. However, these schedulers assume that the model is progressively approaching convergence, which may not always be true, leading to delayed or premature adjustments. In this work, we propose dynamic Learning Rate for deep Reinforcement Learning (LRRL), a meta-learning approach that selects the learning rate based on the agent's performance during training. LRRL is based on a multi-armed bandit algorithm, where each arm represents a different learning rate, and the bandit feedback is provided by the cumulative returns of the RL policy to update the arms' probability distribution. Our empirical results demonstrate that LRRL can substantially improve the performance of deep RL algorithms.

MARVEL: MR Fingerprinting with Additional micRoVascular Estimates using bidirectional LSTMs

The Magnetic Resonance Fingerprinting (MRF) approach aims to estimate multiple MR or physiological parameters simultaneously with a single fast acquisition sequence. Most of the MRF studies proposed so far have used simple MR sequence types to measure relaxation times (T1, T2). In that case, deep learning algorithms have been successfully used to speed up the reconstruction process. In theory, the MRF concept could be used with a variety of other MR sequence types and should be able to provide more information about the tissue microstructures. Yet, increasing the complexity of the numerical models often leads to prohibited simulation times, and estimating multiple parameters from one sequence implies new dictionary dimensions whose sizes become too large for standard computers and DL architectures.In this paper, we propose to analyze the MRF signal coming from a complex balance Steady-state free precession (bSSFP) type sequence to simultaneously estimate relaxometry maps (T1, T2), Field maps (B1, B0) as well as microvascular properties such as the local Cerebral Blood Volume (CBV) or the averaged vessel Radius (R).To bypass the curse of dimensionality, we propose an efficient way to simulate the MR signal coming from numerical voxels containing realistic microvascular networks as well as a Bidirectional Long Short-Term Memory network used for the matching process.On top of standard MRF maps, our results on 3 human volunteers suggest that our approach can quickly produce high-quality quantitative maps of microvascular parameters that are otherwise obtained using longer dedicated sequences and intravenous injection of a contrast agent. This approach could be used for the management of multiple pathologies and could be tuned to provide other types of microstructural information.

On Best-Arm Identification with a Fixed Budget in Non-Parametric Multi-Armed Bandits

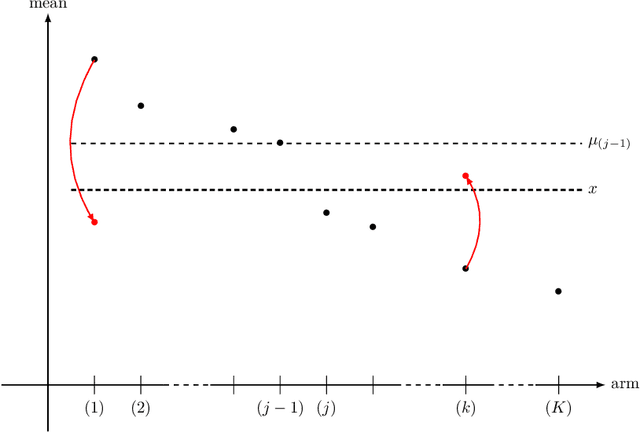
We lay the foundations of a non-parametric theory of best-arm identification in multi-armed bandits with a fixed budget T. We consider general, possibly non-parametric, models D for distributions over the arms; an overarching example is the model D = P(0,1) of all probability distributions over [0,1]. We propose upper bounds on the average log-probability of misidentifying the optimal arm based on information-theoretic quantities that correspond to infima over Kullback-Leibler divergences between some distributions in D and a given distribution. This is made possible by a refined analysis of the successive-rejects strategy of Audibert, Bubeck, and Munos (2010). We finally provide lower bounds on the same average log-probability, also in terms of the same new information-theoretic quantities; these lower bounds are larger when the (natural) assumptions on the considered strategies are stronger. All these new upper and lower bounds generalize existing bounds based, e.g., on gaps between distributions.

A Non-asymptotic Approach to Best-Arm Identification for Gaussian Bandits

We propose a new strategy for best-arm identification with fixed confidence of Gaussian variables with bounded means and unit variance. This strategy called Exploration-Biased Sampling is not only asymptotically optimal: we also prove non-asymptotic bounds occurring with high probability. To the best of our knowledge, this is the first strategy with such guarantees. But the main advantage over other algorithms like Track-and-Stop is an improved behavior regarding exploration: Exploration-Biased Sampling is slightly biased in favor of exploration in a subtle but natural way that makes it more stable and interpretable. These improvements are allowed by a new analysis of the sample complexity optimization problem, which yields a faster numerical resolution scheme and several quantitative regularity results that we believe of high independent interest.