Online Learning with Feedback Graphs: The True Shape of Regret

Sequential learning with feedback graphs is a natural extension of the multi-armed bandit problem where the problem is equipped with an underlying graph structure that provides additional information - playing an action reveals the losses of all the neighbors of the action. This problem was introduced by \citet{mannor2011} and received considerable attention in recent years. It is generally stated in the literature that the minimax regret rate for this problem is of order $\sqrt{\alpha T}$, where $\alpha$ is the independence number of the graph, and $T$ is the time horizon. However, this is proven only when the number of rounds $T$ is larger than $\alpha^3$, which poses a significant restriction for the usability of this result in large graphs. In this paper, we define a new quantity $R^*$, called the \emph{problem complexity}, and prove that the minimax regret is proportional to $R^*$ for any graph and time horizon $T$. Introducing an intricate exploration strategy, we define the \mainAlgorithm algorithm that achieves the minimax optimal regret bound and becomes the first provably optimal algorithm for this setting, even if $T$ is smaller than $\alpha^3$.

On the complexity of All $\varepsilon$-Best Arms Identification

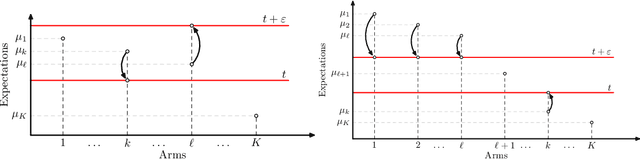
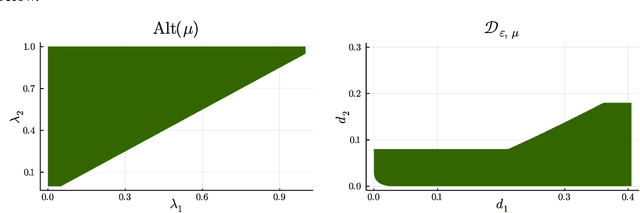
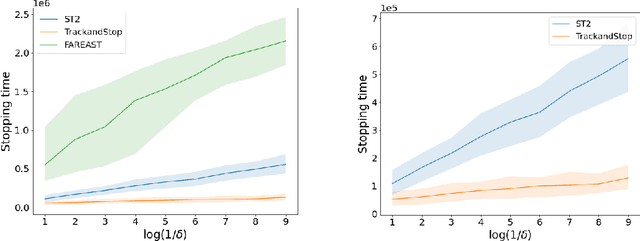
We consider the problem introduced by \cite{Mason2020} of identifying all the $\varepsilon$-optimal arms in a finite stochastic multi-armed bandit with Gaussian rewards. In the fixed confidence setting, we give a lower bound on the number of samples required by any algorithm that returns the set of $\varepsilon$-good arms with a failure probability less than some risk level $\delta$. This bound writes as $T_{\varepsilon}^*(\mu)\log(1/\delta)$, where $T_{\varepsilon}^*(\mu)$ is a characteristic time that depends on the vector of mean rewards $\mu$ and the accuracy parameter $\varepsilon$. We also provide an efficient numerical method to solve the convex max-min program that defines the characteristic time. Our method is based on a complete characterization of the alternative bandit instances that the optimal sampling strategy needs to rule out, thus making our bound tighter than the one provided by \cite{Mason2020}. Using this method, we propose a Track-and-Stop algorithm that identifies the set of $\varepsilon$-good arms w.h.p and enjoys asymptotic optimality (when $\delta$ goes to zero) in terms of the expected sample complexity. Finally, using numerical simulations, we demonstrate our algorithm's advantage over state-of-the-art methods, even for moderate values of the risk parameter.

A Non-asymptotic Approach to Best-Arm Identification for Gaussian Bandits

We propose a new strategy for best-arm identification with fixed confidence of Gaussian variables with bounded means and unit variance. This strategy called Exploration-Biased Sampling is not only asymptotically optimal: we also prove non-asymptotic bounds occurring with high probability. To the best of our knowledge, this is the first strategy with such guarantees. But the main advantage over other algorithms like Track-and-Stop is an improved behavior regarding exploration: Exploration-Biased Sampling is slightly biased in favor of exploration in a subtle but natural way that makes it more stable and interpretable. These improvements are allowed by a new analysis of the sample complexity optimization problem, which yields a faster numerical resolution scheme and several quantitative regularity results that we believe of high independent interest.

Best Arm Identification in Spectral Bandits

We study best-arm identification with fixed confidence in bandit models with graph smoothness constraint. We provide and analyze an efficient gradient ascent algorithm to compute the sample complexity of this problem as a solution of a non-smooth max-min problem (providing in passing a simplified analysis for the unconstrained case). Building on this algorithm, we propose an asymptotically optimal strategy. We furthermore illustrate by numerical experiments both the strategy's efficiency and the impact of the smoothness constraint on the sample complexity. Best Arm Identification (BAI) is an important challenge in many applications ranging from parameter tuning to clinical trials. It is now very well understood in vanilla bandit models, but real-world problems typically involve some dependency between arms that requires more involved models. Assuming a graph structure on the arms is an elegant practical way to encompass this phenomenon, but this had been done so far only for regret minimization. Addressing BAI with graph constraints involves delicate optimization problems for which the present paper offers a solution.